题目内容
【题目】如图,P为反比例函数![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )

A. 2 B. 4 C. 6 D. 8
【答案】D
【解析】设一次函数y=-x-4交y轴于点C.
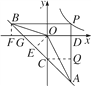
如图,作BF⊥x轴,OE⊥AB,CQ⊥AP,设P点坐标![]() .
.
∵直线AB的解析式为y=-x-4,PB⊥y轴,PA⊥x轴,
∴∠PBA=∠PAB=45°,
∴PA=PB.
∵P点坐标为![]() ,
,
∴OD=CQ=n.
∵当x=0时,y=-x-4=-4,
∴OC=DQ=4,
∴AD=AQ+DQ=n+4.
GE=OE=![]() OC=2
OC=2![]() .
.
同理得BG=![]() BF=
BF=![]() PD=
PD=![]() ,
,
∴BE=BG+EG=![]() +2
+2![]() .
.
∵∠AOB=135°,
∴∠OBE+∠OAE=45°.
∵∠DAO+∠OAE=45°,
∴∠DAO=∠OBE.
又∵∠BEO=∠ADO=90°,
∴△BOE∽△AOD,
∴![]() =
=![]() ,即
,即![]() =
= ,
,
∴k=8.
故选D.

练习册系列答案
相关题目

