题目内容
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
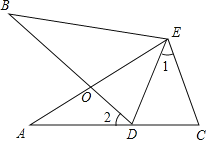
(1)求证:∠BDE=∠C;
(2)求证:△AEC≌△BED;
(3)若∠2=40°,则∠BDE=______°.
【答案】(1)见解析,(2)见解析;(3)∠BDE=70°
【解析】
(1)根据三角形内角和可以求得∠2和∠BEO的关系,从而可以求得∠BDE和∠C的关系;
(2)根据(1)中的结论和全等三角形的判定即可证明结论成立;
(3)根据等腰三角形的性质和全等三角形的性质可以求得∠BDE的度数.
解:(1)证明:

∵∠B=∠A,∠AOD=∠BOE,
∴∠2=∠BEO,
∵∠1=∠2,
∴∠BEO=∠1,
∴∠BED=∠AEC,
又∵∠B=∠A,
∴∠BDE=∠C;
(2)证明:由(1)知∠BDE=∠C,在△AEC和△BED中,
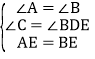 ,
,
∴△AEC≌△BED(AAS);
(3)由(2)知△AEC≌△BED,
∴ED=EC,
∴∠EDC=∠ECD,
∵∠2=40°,∠1=∠2,
∴∠1=40°,
∴∠EDC=∠ECD=70°,
∴∠BDE=180°-∠2-∠EDC=180°-40°-70°=70°,

练习册系列答案
相关题目