题目内容
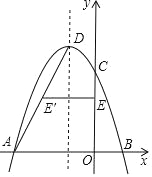
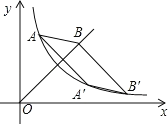
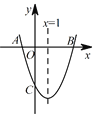
【题目】如图,抛物线y1=![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B,C两点,且D,E分别为顶点.则下列结论:
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B,C两点,且D,E分别为顶点.则下列结论:

①a=![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时y1>y2.
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时y1>y2.
其中正确的结论是( )
A. ①③④ B. ①③ C. ①②④ D. ②
【答案】B
【解析】
把点A坐标代入y2,求出a的值,即可得到函数解析式;令y=3,求出A、B、C的横坐标,然后求出BD、AD的长,利用勾股定理的逆定理以及结合二次函数图象分析得出答案.
抛物线y1=![]() (x+1)2+1与y2=a(x-4)2-3交于点A(1,3),
(x+1)2+1与y2=a(x-4)2-3交于点A(1,3),
∴3=a(1-4)2-3,
解得:a=![]() ,故①正确;
,故①正确;
过点E作EF⊥AC于点F,
∵E是抛物线的顶点,
∴AE=EC,E(4,-3),
∴AF=3,EF=6,
∴AE=![]() ,AC=2AF=6,
,AC=2AF=6,
∴AC≠AE,故②错误;
当y=3时,3=![]() (x+1)2+1,
(x+1)2+1,
解得:x1=1,x2=-3,
故B(-3,3),D(-1,1),
则AB=4,AD=BD=2![]() ,
,
∴AD2+BD2=AB2,
∴③△ABD是等腰直角三角形,正确;
∵![]() (x+1)2+1=
(x+1)2+1=![]() (x-4)2-3时,
(x-4)2-3时,
解得:x1=1,x2=37,
∴当37>x>1时,y1>y2,故④错误.
故选:B.

练习册系列答案
相关题目