题目内容
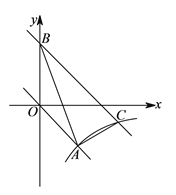
【题目】如图,四边形是平行四边形,以AB为直径的![]() 经过点D, E是
经过点D, E是![]() 上一点,且
上一点,且![]() .
.
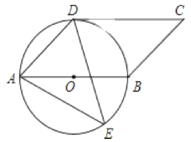
(1)判断CD与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2) 若BC=2 .求阴影部分的面积.(结果保留π 的形式).
【答案】(1)相切,证明见解析(2)3-![]() π.
π.
【解析】
(1)连接BD,OD求出∠ABD=∠AED=45°,根据DC∥AB推出∠CDB=45°求出∠ODC=90°根据切线的判定推出即可
(2)求出∠AOD=∠BOD=90°,求出AO,OD分别求出△AOD扇形DOB,平行四边形ABCD的面积相减即可求出答案
(1)解CD与⊙O的位置关系是相切
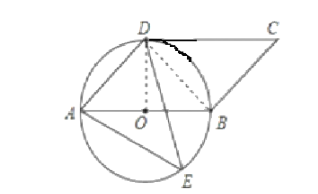
理由是连接BD,OD
∵∠AED=45°
∴∠ABD=∠AED=45°
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=45°
∵OD=OB,
∴∠ODB=∠OBD=45°
∴∠ODC=45°+45°=90°
∵OD为半径,
∴CD与⊙O的位置关系是相切;
(2)解AB∥CD,∠ODC=90°
∴∠DOB=90°=∠DOA,
∵四边形ABCD是平行四边形,
∴AD=BC=2,
在△AOD中由勾股定理得:2AO![]() =2
=2![]()
AO=OD=OB=![]() ,
,
∴S△AOD=![]() OA×OD=
OA×OD=![]() ×
×![]() ×
×![]() =1,
=1,
S扇形BOD=![]()
S平行四边形ABCD=AB×DO=2![]() ×
×![]() =4,
=4,
∴阴影部分的面积是:4-1-![]() π=3-
π=3-![]() π.
π.

练习册系列答案
相关题目