题目内容
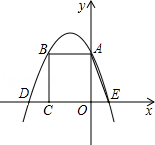
已知抛物线y=-x2+1的顶点为P,点A是第一象限内该二次函数图像上一点,过点A作x轴的平行线交二次函数图像于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA相似吗?
A.始终不相似 B.始终相似
C.只有AB=AD时相似 D.无法确定
B.
解析试题分析:设A(x,-x2+1)根据题意可求出PA、PD、PE的值,从而得出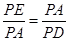 ,又∠APE=∠DPA,因此,△PAD∽△PEA.
,又∠APE=∠DPA,因此,△PAD∽△PEA.
故选B.
考点: 二次函数综合题.

练习册系列答案
相关题目
如图,抛物线y=ax2+bx+c与x轴的负半轴交于点A,B(点A在点B的右边),与y轴的正半轴交于点C,且OA=OC=1,则下列关系中正确的是( )
| A.a+b=1 | B.b<2a | C.a-b=-1 | D.ac<0 |
抛物线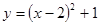 的对称轴是( )
的对称轴是( )
A.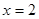 | B. | C.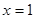 | D.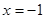 |
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
| A.-1<x<5 | B.x>5 |
| C.x<-1且x>5 | D.x<-1或x>5 |
已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当-5≤x≤0时,下列说法正确的是( )
| A.有最小值-5、最大值0 |
| B.有最小值-3、最大值6 |
| C.有最小值0、最大值6 |
| D.有最小值2、最大值6 |
抛物线y=3x2,y=-3x2,y= x2+3共有的性质是
x2+3共有的性质是
| A.开口向上 | B.对称轴是y轴 |
| C.都有最高点 | D.y随x值的增大而增大 |
 经过平移得到抛物线
经过平移得到抛物线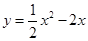 ,其对称轴与两段抛物线所围成的阴影部分的面积为( )
,其对称轴与两段抛物线所围成的阴影部分的面积为( )