题目内容
(2004•福州)如图,在边长为4的正方形ABCD中,E是DC中点,点F在BC边上,且CF=1,在△AEF中作正方形A1B1C1D1,使边A1B1在AF上,其余两个顶点C1、D1分别在EF和AE上.(1)请直接写出图中两直角边之比等于1:2的三个直角三角形(不另添加字母及辅助线);
(2)求AF的长及正方形A1B1C1D1的边长;
(3)在(2)的条件下,取出△AEF,将△EC1D1沿直线C1D1、△C1FB1沿直线C1B1分别向正方形A1B1C1D1内折叠,求小正方形A1B1C1D1未被两个折叠三角覆盖的四边形面积.

【答案】分析:(1)图中满足直角边之比等于1:2的直角三角形共有6个,Rt△CEF与Rt△ADE比较明显,打开找出另外四个之一的“缺口”是证出∠AEF=90°.下面给出两种思路:思路一是先证出△ADE∽△ECF,得到∠FEC=∠EAD,结合Rt△ADE中有∠DEA+∠EAD=90°,可得∠DEA+∠FEC=90°,从而∠AEF=90°.思路二是在△ADE、△ECF和△ABF中分别使用勾股定理求出AE、EF和AF的长,再由勾股定理的逆定理证出∠AEF=90°;
(2)由EM×AF=AE×EF=2S△AEF可以求出EM=2,另外由△D1C1E∽△AFE得出 是利用了“相似三角形对应高的比等于相似比”这一性质,这也是解决形如图2问题的基本方法.该小题如果注意到△AA1D1与△C1B1F都是直角边之比等于1:2的直角三角形的话,不添辅助线也可得出答案:设正方形A1B1C1D1的边长为x,则AA1=2x,B1F=
是利用了“相似三角形对应高的比等于相似比”这一性质,这也是解决形如图2问题的基本方法.该小题如果注意到△AA1D1与△C1B1F都是直角边之比等于1:2的直角三角形的话,不添辅助线也可得出答案:设正方形A1B1C1D1的边长为x,则AA1=2x,B1F= x,因为AA1+A1B1+B1F=AF=5,所以2x+x+
x,因为AA1+A1B1+B1F=AF=5,所以2x+x+ x=5,解得正方形的边长x=
x=5,解得正方形的边长x= ;
;
(3)如何说明△EC1D1沿直线C1D1、△C1FB1沿直线C1B1分别向正方形A1B1C1D1内折叠以后两个三角形的交界处既不重叠又没有空隙是一个难点,比较容易忽略,值得引起重视.下面给出一种另解供参考:由△E1C1D1、△C1B1F1分别由△EC1D1、△C1FB1折叠而成,可得∠3=∠4、∠1=∠2,因为正方形A1B1C1D1中有∠D1C1B1=90°,所以∠4+∠1=180°-90°=90°,即∠2+∠3=90°=∠D1C1B1,从而C1E1与C1F1重合在一条直线上(或三点C1、E1、F1在一条直线上).
解答: 解:(1)Rt△CEF、Rt△ADE、Rt△AEF、Rt△AA1D1、
解:(1)Rt△CEF、Rt△ADE、Rt△AEF、Rt△AA1D1、
Rt△ED1C1、Rt△C1B1F.(写出其中三个即可)
(2)AF= =5
=5
过E作EM⊥AF,垂足为M,交D1C1于N,则
∵AD=4,DE=EC=2,CF=1,
∴EF= ,AE=
,AE= =2
=2 ,
,
∵EM×AF=AE×EF=2S△AEF,即5EM= ×2
×2 ,
,
∴EM=2,
∵四边形A1B1C1D1是正方形
∴D1C1∥AF
∴△D1C1E∽△AFE
∴
设正方形A1B1C1D1的边长为x,则

解得x=
∴正方形A1B1C1D1的边长为 .
.
(3)∵D1C1= ,EN=2-
,EN=2- =
=
∴S△D1EC1= ×
× ×
× =
=
∴ =
= ,C1B1=
,C1B1=
∴B1F=
∴S△C1B1F1= ×
× ×
× =
=
∵∠1=∠2,∠1+∠4=90°,∠2+∠3=90°
∴∠3=∠4
∴E1点在C1F1上
又∵ =(
=( )2=
)2=
∴S未被覆盖四边形= -
- -
- =
= .
.
点评:本题主要考查学生抽象思维能力,错误的主要原因是空间观念以及转化的能力不强,缺乏逻辑推理能力,需要在平时生活中多加培养.
(2)由EM×AF=AE×EF=2S△AEF可以求出EM=2,另外由△D1C1E∽△AFE得出
 是利用了“相似三角形对应高的比等于相似比”这一性质,这也是解决形如图2问题的基本方法.该小题如果注意到△AA1D1与△C1B1F都是直角边之比等于1:2的直角三角形的话,不添辅助线也可得出答案:设正方形A1B1C1D1的边长为x,则AA1=2x,B1F=
是利用了“相似三角形对应高的比等于相似比”这一性质,这也是解决形如图2问题的基本方法.该小题如果注意到△AA1D1与△C1B1F都是直角边之比等于1:2的直角三角形的话,不添辅助线也可得出答案:设正方形A1B1C1D1的边长为x,则AA1=2x,B1F= x,因为AA1+A1B1+B1F=AF=5,所以2x+x+
x,因为AA1+A1B1+B1F=AF=5,所以2x+x+ x=5,解得正方形的边长x=
x=5,解得正方形的边长x= ;
;(3)如何说明△EC1D1沿直线C1D1、△C1FB1沿直线C1B1分别向正方形A1B1C1D1内折叠以后两个三角形的交界处既不重叠又没有空隙是一个难点,比较容易忽略,值得引起重视.下面给出一种另解供参考:由△E1C1D1、△C1B1F1分别由△EC1D1、△C1FB1折叠而成,可得∠3=∠4、∠1=∠2,因为正方形A1B1C1D1中有∠D1C1B1=90°,所以∠4+∠1=180°-90°=90°,即∠2+∠3=90°=∠D1C1B1,从而C1E1与C1F1重合在一条直线上(或三点C1、E1、F1在一条直线上).
解答:
 解:(1)Rt△CEF、Rt△ADE、Rt△AEF、Rt△AA1D1、
解:(1)Rt△CEF、Rt△ADE、Rt△AEF、Rt△AA1D1、Rt△ED1C1、Rt△C1B1F.(写出其中三个即可)
(2)AF=
 =5
=5过E作EM⊥AF,垂足为M,交D1C1于N,则
∵AD=4,DE=EC=2,CF=1,
∴EF=
 ,AE=
,AE= =2
=2 ,
,∵EM×AF=AE×EF=2S△AEF,即5EM=
 ×2
×2 ,
,∴EM=2,
∵四边形A1B1C1D1是正方形
∴D1C1∥AF
∴△D1C1E∽△AFE
∴

设正方形A1B1C1D1的边长为x,则

解得x=

∴正方形A1B1C1D1的边长为
 .
.(3)∵D1C1=
 ,EN=2-
,EN=2- =
=
∴S△D1EC1=
 ×
× ×
× =
=
∴
 =
= ,C1B1=
,C1B1=
∴B1F=

∴S△C1B1F1=
 ×
× ×
× =
=
∵∠1=∠2,∠1+∠4=90°,∠2+∠3=90°
∴∠3=∠4
∴E1点在C1F1上
又∵
 =(
=( )2=
)2=
∴S未被覆盖四边形=
 -
- -
- =
= .
.点评:本题主要考查学生抽象思维能力,错误的主要原因是空间观念以及转化的能力不强,缺乏逻辑推理能力,需要在平时生活中多加培养.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
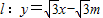 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.

 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.

 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.