题目内容
(2004•福州)如图所示,l1和l2分别表示一种白炽灯和一种节能灯的费用y(元)与照明时间x(小时)的函数关系图象,假设两种灯的使用寿命都是2000小时,照明效果一样.(费用=灯的售价+电费)(1)根据图象分别求出l1,l2的函数关系式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法.

【答案】分析:(1)根据l1经过点(0,2)、(500,17),得方程组解之可求出解析式,同理l2过(0,20)、(500,26),易求解析式;
(2)费用相等即y1=y2,解方程求出时间;
(3)求出交点坐标,结合函数图象回答问题.
解答:解:(1)设L1的解析式为y1=k1x+b1,L2的解析式为y2=k2x+b2,
由图可知L1过点(0,2),(500,17),
∴
∴k1=0.03,b1=2,
∴y1=0.03x+2(0≤x≤2000),
由图可知L2过点(0,20),(500,26),
同理y2=0.012x+20(0≤x≤2000);
(2)若两种费用相等,
即y1=y2,
则0.03x+2=0.012x+20,
解得x=1000,
∴当x=1000时,两种灯的费用相等;
(3)时间超过1000小时,故前2000h用节能灯,剩下的500h,用白炽灯.
点评:此题旨在检测一次函数解析式的待定系数法及其与方程、不等式的关系.结合函数图象解不等式更具直观性,对方案决策很有帮助,这就是数形结合的优越性.
(2)费用相等即y1=y2,解方程求出时间;
(3)求出交点坐标,结合函数图象回答问题.
解答:解:(1)设L1的解析式为y1=k1x+b1,L2的解析式为y2=k2x+b2,
由图可知L1过点(0,2),(500,17),
∴

∴k1=0.03,b1=2,
∴y1=0.03x+2(0≤x≤2000),
由图可知L2过点(0,20),(500,26),
同理y2=0.012x+20(0≤x≤2000);
(2)若两种费用相等,
即y1=y2,
则0.03x+2=0.012x+20,
解得x=1000,
∴当x=1000时,两种灯的费用相等;
(3)时间超过1000小时,故前2000h用节能灯,剩下的500h,用白炽灯.
点评:此题旨在检测一次函数解析式的待定系数法及其与方程、不等式的关系.结合函数图象解不等式更具直观性,对方案决策很有帮助,这就是数形结合的优越性.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
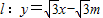 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.
 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.

 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.