题目内容
(2004•福州)如图所示,抛物线y=-(x-m)2的顶点为A,直线 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.(1)写出抛物线对称轴及顶点A的坐标;(用含有m的代数式表示)
(2)证明点A在直线l上,并求∠OAB的度数;
(3)动点Q在抛物线的对称轴上,在对称轴左侧的抛物线上是否存在点P,使以P、Q、A为顶点的三角形与△OAB全等?若存在,求出m的值,并写出所有符合上述条件的P点坐标;若不存在,说明理由.

【答案】分析:(1)根据顶点式抛物线解析式即可得出抛物线的对称轴为x=m,顶点坐标A(m,0);
(2)将A点的坐标代入直线l的解析式中即可判定出点A是否在直线l上.
根据题意不难得出OA=m,OB=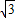 m,据此可求出∠OAB的正切值,进而可求出∠OAB的度数;
m,据此可求出∠OAB的正切值,进而可求出∠OAB的度数;
(3)本题要分四种情况进行讨论:
①当∠AQP=90°,∠QAP=60°,m=3,P点的坐标为(3-3 ,-3);
,-3);
②当∠AQP=90°,∠QPA=60°,m= ,P点的坐标为(0,-3);
,P点的坐标为(0,-3);
③当∠APQ=90°,∠QAP=60°,m= ,P点的坐标为(
,P点的坐标为(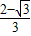 ,-
,- );
);
④当∠APQ=90°,∠AQP=60°,m= ,因此P点的坐标为(-
,因此P点的坐标为(- ,-
,- ).
).
解答:解:(1)对称轴为直线x=m,顶点A(m,0);
(2)把x=m代入函数y= x-
x- m,
m,
得y= m-
m- m=0
m=0
∴点A(m,0)在直线l上.
当x=0时,y=- m
m
∴B(0,- m),tan∠OAB=
m),tan∠OAB=
∴∠OAB=60°;
(3)①当∠AQP=90°,∠QAP=60°,AQ=OA=m,PQ=OB= m
m
,因此P点坐标为(m- m,-m),
m,-m),
将P点的坐标代入抛物线的解析式可得m= ,
,
因此P点的坐标为( ,-
,- ).
).
②当∠AQP=90°,∠QPA=60°,此时P,B重合,
因此P点坐标为(0,- m),
m),
代入抛物线解析式得m= ,因此P点的坐标为(0,-3).
,因此P点的坐标为(0,-3).
③当∠APQ=90°,∠QAP=60°,PA=m,过P作PC⊥AQ于C,
那么PC=AP•sin60°= m,AC=
m,AC= m,
m,
因此P点的坐标为(m- m,-
m,- m).
m).
代入抛物线得m= ,因此P点的坐标为(
,因此P点的坐标为( ,-
,- );
);
④当∠APQ=90°,∠AQP=60°,PA=OB= m,
m,
过P作PD⊥AQ于D,
 那么PD=AP•sin30°=
那么PD=AP•sin30°= m,AD=
m,AD= m,
m,
因此P点的坐标为(m- m,-
m,- m),
m),
代入抛物线得m= ,
,
因此P点的坐标为(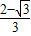 ,-1).
,-1).
点评:本题考查了二次函数的性质及全等三角形的判定等知识点,(3)在不确定全等三角形的对应角和对应边的情况下要分类讨论.
(2)将A点的坐标代入直线l的解析式中即可判定出点A是否在直线l上.
根据题意不难得出OA=m,OB=
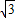 m,据此可求出∠OAB的正切值,进而可求出∠OAB的度数;
m,据此可求出∠OAB的正切值,进而可求出∠OAB的度数;(3)本题要分四种情况进行讨论:
①当∠AQP=90°,∠QAP=60°,m=3,P点的坐标为(3-3
 ,-3);
,-3);②当∠AQP=90°,∠QPA=60°,m=
 ,P点的坐标为(0,-3);
,P点的坐标为(0,-3);③当∠APQ=90°,∠QAP=60°,m=
 ,P点的坐标为(
,P点的坐标为(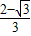 ,-
,- );
);④当∠APQ=90°,∠AQP=60°,m=
 ,因此P点的坐标为(-
,因此P点的坐标为(- ,-
,- ).
).解答:解:(1)对称轴为直线x=m,顶点A(m,0);
(2)把x=m代入函数y=
 x-
x- m,
m,得y=
 m-
m- m=0
m=0∴点A(m,0)在直线l上.
当x=0时,y=-
 m
m∴B(0,-
 m),tan∠OAB=
m),tan∠OAB=
∴∠OAB=60°;
(3)①当∠AQP=90°,∠QAP=60°,AQ=OA=m,PQ=OB=
 m
m,因此P点坐标为(m-
 m,-m),
m,-m),将P点的坐标代入抛物线的解析式可得m=
 ,
,因此P点的坐标为(
 ,-
,- ).
).②当∠AQP=90°,∠QPA=60°,此时P,B重合,
因此P点坐标为(0,-
 m),
m),
代入抛物线解析式得m=
 ,因此P点的坐标为(0,-3).
,因此P点的坐标为(0,-3).③当∠APQ=90°,∠QAP=60°,PA=m,过P作PC⊥AQ于C,
那么PC=AP•sin60°=
 m,AC=
m,AC= m,
m,因此P点的坐标为(m-
 m,-
m,- m).
m).代入抛物线得m=
 ,因此P点的坐标为(
,因此P点的坐标为( ,-
,- );
);④当∠APQ=90°,∠AQP=60°,PA=OB=
 m,
m,过P作PD⊥AQ于D,
 那么PD=AP•sin30°=
那么PD=AP•sin30°= m,AD=
m,AD= m,
m,因此P点的坐标为(m-
 m,-
m,- m),
m),代入抛物线得m=
 ,
,因此P点的坐标为(
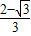 ,-1).
,-1).点评:本题考查了二次函数的性质及全等三角形的判定等知识点,(3)在不确定全等三角形的对应角和对应边的情况下要分类讨论.

练习册系列答案
相关题目
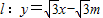 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.

 与y轴的交点为B,其中m>0.
与y轴的交点为B,其中m>0.
