题目内容
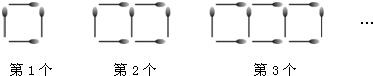
如图所示,是一列用若干根火柴棒摆成的由正方形组成的图案.
(1)完成下表的填空:
| 正方形个数 | 1 | 2 | 3 | 4 | 5 | 6 | n |
| 火柴棒根数 | 4 | 7 | 10 | 13 |
解:(1)按如图的方式摆放,每增加1个正方形火花图案,火柴棒的根数相应地增加3根,
若摆成5个、6个、n个同样大小的正方形火花图案,则相应的火柴棒的根数分别是16根、19根、(3n+1)根.
(2)
∵当他摆完第n个图案时剩下了20根火柴棒,要刚好摆完第n+1个图案还差2根.
∴3(n+1)+1=22,
解得n=6,
∴这位同学最后摆的图案是第7个图案.
分析:(1)易得组成一个正方形都需要4根火柴棒,找到组成1个以上的正方形需要的火柴棒的根数在4的基础上增加几个3即可.
(2)根据(1)的规律得出3(n+1)+1=22,解出n即可.
点评:本题考查图形的规律性问题;得到不变的量及变化的量与n的关系是解决本题的关键.
若摆成5个、6个、n个同样大小的正方形火花图案,则相应的火柴棒的根数分别是16根、19根、(3n+1)根.
| 正方形个数 | 1 | 2 | 3 | 4 | 5 | 6 | n |
| 火柴棒根数 | 4 | 7 | 10 | 13 | 16 | 19 | 3n+1 |
∵当他摆完第n个图案时剩下了20根火柴棒,要刚好摆完第n+1个图案还差2根.
∴3(n+1)+1=22,
解得n=6,
∴这位同学最后摆的图案是第7个图案.
分析:(1)易得组成一个正方形都需要4根火柴棒,找到组成1个以上的正方形需要的火柴棒的根数在4的基础上增加几个3即可.
(2)根据(1)的规律得出3(n+1)+1=22,解出n即可.
点评:本题考查图形的规律性问题;得到不变的量及变化的量与n的关系是解决本题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
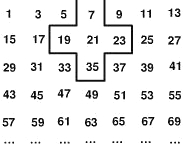
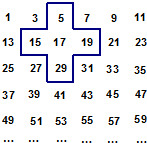 将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.
将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.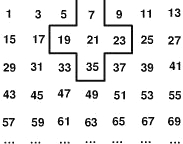
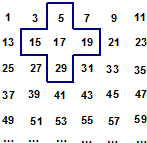 将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.
将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.