题目内容
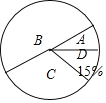
【题目】已知:如图,⊙O的两条半径OA⊥OB,C,D是![]() 的三等分点,OC,OD分别与AB相交于点E,F.
的三等分点,OC,OD分别与AB相交于点E,F.
求证:CD=AE=BF.

【答案】见解析
【解析】
连接AC、BD,由C,D是![]() 的三等分点,可得AC=CD=BD,∠AOC=∠COD=∠DOB=30°,利用SAS可证明△AOC≌△COD,即可得出∠ACO=∠OCD,根据等腰三角形的性质可得∠OEF=∠OCD,可证明CD//AB,可得∠AEC=∠OCD,即可证明∠ACO=∠AEC.可得AC=AE,同理可证BD=BF,进而可证明CD=AE=BF.
的三等分点,可得AC=CD=BD,∠AOC=∠COD=∠DOB=30°,利用SAS可证明△AOC≌△COD,即可得出∠ACO=∠OCD,根据等腰三角形的性质可得∠OEF=∠OCD,可证明CD//AB,可得∠AEC=∠OCD,即可证明∠ACO=∠AEC.可得AC=AE,同理可证BD=BF,进而可证明CD=AE=BF.
连接AC、BD,
∵OA⊥OB,
∴∠AOB=90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵C,D是![]() 的三等分点,
的三等分点,
∴AC=CD=BD,∠AOC=∠COD=∠DOB=30°,
∵∠AOC=∠COD,OA=OC=OD,
∴△AOC≌△COD,
∴∠ACO=∠OCD,
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD=![]() =75°,
=75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
故AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴CD=AE=BF.


练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】某市将开展演讲比赛活动,某校对参加选拔的学生的成绩按A、B、C、D四个等级进行统计,绘制了如下不完整的统计表和扇形统计图,
成绩等级 | 频数 | 频率 |
A | 4 | n |
B | m | 0.51 |
C | ||
D | 15 |
(1)求m、n的值;
(2)求“C等级”所对应的扇形圆心角的度数;
(3)已知成绩等级为A的4名学生中有1名男生和3名女生,现从中随机挑选2名学生代表学校参加全市比赛,求出恰好选中一男生和一女生的概率