题目内容
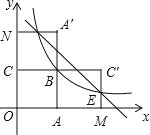
【题目】如图,四边形OABC是边长为2的正方形,函数y=![]() (k>0)的图象经过点B,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′,NA′BC.设线段MC′,NA′分别与函数y=
(k>0)的图象经过点B,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′,NA′BC.设线段MC′,NA′分别与函数y=![]() (k>0)的图象交于点E、F,则直线EF与x轴的交点坐标为 .
(k>0)的图象交于点E、F,则直线EF与x轴的交点坐标为 .
【答案】(5,0).
【解析】
试题解析:补充完整图形,如下图所示.
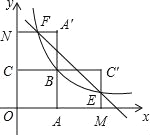
∵四边形OABC是边长为2的正方形,
∴点B的坐标为(2,2),
∵函数y=![]() (k>0)的图象经过点B,
(k>0)的图象经过点B,
∴k=2×2=4,
∴反比例函数解析式为y=![]() .
.
∵将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′,NA′BC,
∴线段MC′所在的直线的解析式为x=4,线段NA′所在的直线的解析式为y=4,
令y=![]() 中x=4,则y=1,
中x=4,则y=1,
∴点E的坐标为(4,1);
令y=![]() 中y=4,则
中y=4,则![]() =4,解得:x=1,
=4,解得:x=1,
∴点F的坐标为(1,4).
设直线EF的解析式为y=ax+b,
∴![]() ,解得:
,解得:![]() ,
,
∴直线EF的解析式为y=-x+5,
令y=-x+5中y=0,则-x+5=0,
解得:x=5,
∴直线EF与x轴的交点坐标为(5,0).

练习册系列答案
相关题目