题目内容
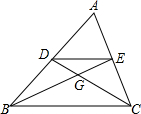 如图,△ABC的中线BE与CD交于点G,连接DE,下列结论不正确的是
如图,△ABC的中线BE与CD交于点G,连接DE,下列结论不正确的是
- A.点G是△ABC的重心
- B.DE∥BC
- C.△ABC的面积=2△ADE的面积
- D.BG=2GE
C
分析:根据DE是△ABC的中位线可判断出选项A、B、C的正确与错误,利用相似三角形面积的比等于相似比的平方可判定选项B.
解答:∵△ABC的中线BE与CD交于点G,
∴点G是△ABC的重心,
∴DE∥BC且DE= BC,所以选项A、B正确;
BC,所以选项A、B正确;
∵点G是△ABC的重心,根据重心性质或利用三角形相似可得BG=2GE,
∴选项D正确;
由△ADE∽△ABC,可知△ABC的面积=4△ADE的面积,
所以选项C错误.
故选C.
点评:此题主要考查学生对三角形中位线定理和三角形重心的理解和掌握,此题难度不大,属于基础题,要求同学们应熟练掌握此题的知识点.
分析:根据DE是△ABC的中位线可判断出选项A、B、C的正确与错误,利用相似三角形面积的比等于相似比的平方可判定选项B.
解答:∵△ABC的中线BE与CD交于点G,
∴点G是△ABC的重心,
∴DE∥BC且DE=
 BC,所以选项A、B正确;
BC,所以选项A、B正确;∵点G是△ABC的重心,根据重心性质或利用三角形相似可得BG=2GE,
∴选项D正确;
由△ADE∽△ABC,可知△ABC的面积=4△ADE的面积,
所以选项C错误.
故选C.
点评:此题主要考查学生对三角形中位线定理和三角形重心的理解和掌握,此题难度不大,属于基础题,要求同学们应熟练掌握此题的知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
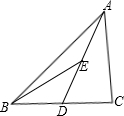 已知如图,△ABC的中线AD的中点为E,S△BDE=2cm2,那么S△ABC=
已知如图,△ABC的中线AD的中点为E,S△BDE=2cm2,那么S△ABC=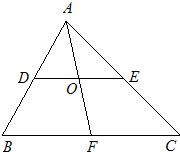 24、如图,△ABC的中线AF与中位线DE相交于点O、试问AF与DE是否互相平分?为什么?
24、如图,△ABC的中线AF与中位线DE相交于点O、试问AF与DE是否互相平分?为什么? 如图,△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.
如图,△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.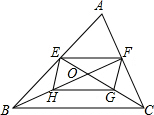 如图,△ABC的中线BF、CE相交于点O,点H、G分别是BO、CO的中点,试判断四边形EFGH的形状,并证明你的结论.
如图,△ABC的中线BF、CE相交于点O,点H、G分别是BO、CO的中点,试判断四边形EFGH的形状,并证明你的结论.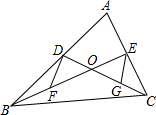 如图,△ABC的中线BE,CD相交于点O,F,G分别是BO、CO的中点,试猜想DF与EG有怎样的数量关系和位置关系?并证明你的猜想.
如图,△ABC的中线BE,CD相交于点O,F,G分别是BO、CO的中点,试猜想DF与EG有怎样的数量关系和位置关系?并证明你的猜想.