题目内容
 如图,△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.
如图,△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:EF=DG且EF∥DG.
分析:根据三角形的中位线推出DE∥BC,DE=
BC,GF∥BC,GF=
BC,推出GF=DE,GF∥DE,得出平行四边形DEFG,根据平行四边形的性推出即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵BD、CE是△ABC的中线,
∴DE∥BC,DE=
BC,
同理:GF∥BC,GF=
BC,
∴GF=DE,GF∥DE,
∴四边形DEFG是平行四边形,
∴EF=DG,EF∥DG.
∴DE∥BC,DE=
| 1 |
| 2 |
同理:GF∥BC,GF=
| 1 |
| 2 |
∴GF=DE,GF∥DE,
∴四边形DEFG是平行四边形,
∴EF=DG,EF∥DG.
点评:本题考查了平行四边形的性质和判定,三角形的中位线,三角形的中线等知识点,主要检查学生能否熟练的运用性质进行推理,题目比较典型,难度适中,通过做此题培养了学生分析问题和解决问题的能力.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
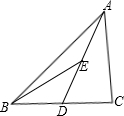 已知如图,△ABC的中线AD的中点为E,S△BDE=2cm2,那么S△ABC=
已知如图,△ABC的中线AD的中点为E,S△BDE=2cm2,那么S△ABC=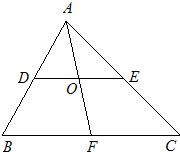 24、如图,△ABC的中线AF与中位线DE相交于点O、试问AF与DE是否互相平分?为什么?
24、如图,△ABC的中线AF与中位线DE相交于点O、试问AF与DE是否互相平分?为什么?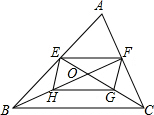 如图,△ABC的中线BF、CE相交于点O,点H、G分别是BO、CO的中点,试判断四边形EFGH的形状,并证明你的结论.
如图,△ABC的中线BF、CE相交于点O,点H、G分别是BO、CO的中点,试判断四边形EFGH的形状,并证明你的结论.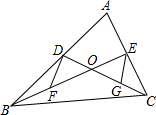 如图,△ABC的中线BE,CD相交于点O,F,G分别是BO、CO的中点,试猜想DF与EG有怎样的数量关系和位置关系?并证明你的猜想.
如图,△ABC的中线BE,CD相交于点O,F,G分别是BO、CO的中点,试猜想DF与EG有怎样的数量关系和位置关系?并证明你的猜想.