题目内容
【题目】在极坐标系中,点 ![]() ,曲线
,曲线 ![]() .以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系. (Ⅰ)在直角坐标系中,求点A,B的直角坐标及曲线C的参数方程;
.以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系. (Ⅰ)在直角坐标系中,求点A,B的直角坐标及曲线C的参数方程;
(Ⅱ)设点M为曲线C上的动点,求|MA|2+|MB|2取值范围.
【答案】解:(I)利用 ![]() ,则点
,则点 ![]() 的直角坐标分别为:A
的直角坐标分别为:A 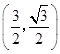 ,B
,B ![]() . 曲线
. 曲线 ![]() .即ρ2=2ρ
.即ρ2=2ρ 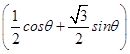 ,化为直角坐标方程:x2+y2﹣x﹣
,化为直角坐标方程:x2+y2﹣x﹣ ![]() y=0.
y=0.
配方为: ![]() +
+ ![]() =1.
=1.
可得参数方程为: 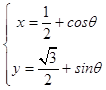 .
.
(II)不妨设M  ,
,
则|MA|2+|MB|2=(cosα﹣1)2+sin2θ+ ![]() +
+ ![]() =4﹣cosα﹣
=4﹣cosα﹣ ![]() sinα=4﹣2sin
sinα=4﹣2sin ![]() .
.
∵sin ![]() ∈[﹣1,1],则4﹣2sin
∈[﹣1,1],则4﹣2sin ![]() ∈[2,6].
∈[2,6].
因此:|MA|2+|MB|2取值范围是[2,6]
【解析】(I)利用 ![]() ,可得A,B直角坐标.曲线
,可得A,B直角坐标.曲线 ![]() .即ρ2=2ρ
.即ρ2=2ρ ![]() ,即可化为直角坐标方程,通过配方利用平方关系可得参数方程.(II)不妨设M
,即可化为直角坐标方程,通过配方利用平方关系可得参数方程.(II)不妨设M ![]() ,可得|MA|2+|MB|2=4﹣2sin
,可得|MA|2+|MB|2=4﹣2sin ![]() .利用sin
.利用sin ![]() ∈[﹣1,1],即可得出.
∈[﹣1,1],即可得出.

练习册系列答案
相关题目