题目内容
 探索研究:
探索研究:已知A,B在数轴上分别表示a、b.利用数形结合思想回答下列问题:
(1)填写下表:
| 数 | 列A | 列B | 列C | 列D | 列E | 列F |
| a | 5 | -5 | -6 | -6 | -10 | -2.5 |
| b | 3 | 0 | 4 | -4 | 2 | -2.5 |
| A,B两点的距离 | 2 | 10 | 5 |
|x+2|
|x+2|
.(3)若A,B两点的距离为d,则d与a、b有何数量关系:
d=|a-b|
d=|a-b|
.(4)若x表示一个有理数,且-3<x<1,则|x-1|+|x+3|=
4
4
.分析:(1)首先要明确两点间的距离,即为两数差的绝对值得出即可.
(2)通过观察研究可知:数轴上表示x和-2的两点之间的距离;
(3)明确两点间的距离,即为两数差的绝对值(d=|a-b|);
(4)由-3<x<1得,|x-1|+|x+3|实际是-3与1的距离,得出即可.
(2)通过观察研究可知:数轴上表示x和-2的两点之间的距离;
(3)明确两点间的距离,即为两数差的绝对值(d=|a-b|);
(4)由-3<x<1得,|x-1|+|x+3|实际是-3与1的距离,得出即可.
解答:解:(1)填表如下:
(2)|x-(-2)|=|x+2|;
故答案为:|x+2|;
(3)根据题意得出:d=|a-b|.
故答案为:d=|a-b|;
(4)根据题意得出:∵-3<x<1,
∴|x-1|+|x+3|=|1+3|=4.
故答案为:4.
| 数 | 列A | 列B | 列C | 列D | 列E | 列F |
| a | 5 | -5 | -6 | -6 | -10 | -2.5 |
| b | 3 | 0 | 4 | -4 | 2 | -2.5 |
| A,B两点的距离 | 2 | 5 | 10 | 2 | 12 | 0 |
故答案为:|x+2|;
(3)根据题意得出:d=|a-b|.
故答案为:d=|a-b|;
(4)根据题意得出:∵-3<x<1,
∴|x-1|+|x+3|=|1+3|=4.
故答案为:4.
点评:本题主要考查的是数的绝对值,首先要牢记绝对值的定义以及几何和代数的意义.

练习册系列答案
相关题目
 探索研究
探索研究已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -5 | -8 | -9 | -8 | … |
(2)若A(m,y1),B(m+4,y2)两点都在该函数的图象上.
①试比较y1与y2的大小;
②若A、B两点位于x轴的下方,点P为函数图象的对称轴与x轴的交点,点Q为函数图象上的一点,解答以下问题:
(Ⅰ)直接写出实数m的变化范围是
(Ⅱ)是否存在实数m,使得四边形APBQ为平行四边形?若存在,请求出m的值,并写出点Q的坐标;若不存在,请说明理由.
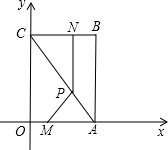 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒. (2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数
(2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数 (2012•营口一模)[提出问题]:已知矩形的面积为1,当该矩形的长为多少时,它的周长最小?最小值是多少?
(2012•营口一模)[提出问题]:已知矩形的面积为1,当该矩形的长为多少时,它的周长最小?最小值是多少?