Question

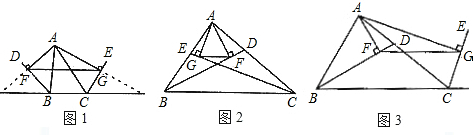
如图1，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F、G，连接FG，延长AF、AG，与直线BC相交于M、N．
（1）试说明：FG=

1

2

（AB+BC+AC）；
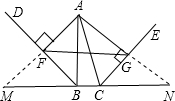
（2）如图2，若BD、CE分别是△ABC的内角平分线，则线段FG与△ABC三边又有怎样的数量关系？请写出你的猜想，并对其中的一种情况说明理由；
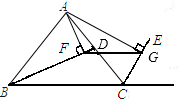
（3）如图3，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，则线段FG与△ABC三边的数量关系是

 

．

Answer 1

分析：（1）推出∠AFB=∠MFB，证△ABF≌△MBF，进一步推出MB=AB，AF=MF，同理CN=AC，AG=NG，即可得出答案；
（2）延长AF、AG，与直线BC相交于M、N，与（1）类似可以证出答案；
（3）与（1）方法类同即可证出答案．

解答：解：（1）∵BD⊥AF，
∴∠AFB=∠MFB=90°，
在△ABF和△MBF中

∠AFB=∠MFB BF=BF ∠ABF=∠MBF

，
∴△ABF≌△MBF（ASA）
∴MB=AB
∴AF=MF，
同理：CN=AC，AG=NG，
∴FG是△AMN的中位线
∴FG=

1

2

MN，
=

1

2

（MB+BC+CN），
=

1

2

（AB+BC+AC）．

（2）图（2）中，FG=

1

2

（AB+AC-BC）
解：如图（2），
延长AF、AG，与直线BC相交于M、N，
∵AF⊥BD，∠ABF=∠MBF，
∴∠BAF=∠BMF，
在△ABF和△MBF中
∵

∠AFB=∠MFB BF=BF ∠ABF=∠MBF

，
∴△ABF≌△MBF（ASA）
∴MB=AB，AF=MF，
同理：CN=AC，AG=NG
∴FG=

1

2

MN，
=

1

2

（BM+CN-BC），
=

1

2

（AB+AC-BC），
答：线段FG与△ABC三边的数量关系是FG=

1

2

（AB+AC-BC）．

（3）解：FG=

1

2

（AC+BC-AB），
理由是：∵AF⊥BD，∠ABF=∠MBF，
∴∠BAF=∠BMF，
在△ABF和△MBF中
∵

∠AFB=∠MFB BF=BF ∠ABF=∠MBF

，
∴△ABF≌△MBF（ASA）
∴MB=AB，AF=MF，
同理：CN=AC，AG=NG
∴FG=

1

2

MN，
=

1

2

（CN+BC-BM），
=

1

2

（AC+BC-AB）．
故答案为：FG=

1

2

（AC+BC-AB）．

点评：本题主要考查了三角形的中位线定理，三角形的内角和定理，等腰三角形的性质和判定等知识点，解此题的关键是作辅助线转化成三角形的中位线．