题目内容
【题目】已知抛物线![]() ,通过画图发现,无论b取何值,抛物线总会经过两个定点;
,通过画图发现,无论b取何值,抛物线总会经过两个定点;
(1)直接写出这两个定点的坐标________ ,_________;
(2)若将此抛物线向右平移![]() 单位,再向上平移
单位,再向上平移![]() (b>0)个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
(b>0)个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
(3)若抛物线![]() 与直线y=x–3有两个交点A与B,且
与直线y=x–3有两个交点A与B,且![]() ,求b的取值范围.
,求b的取值范围.
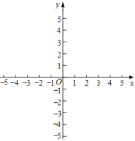
【答案】(1)(0,-3),(-1,0);(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)y=bx2+(b3)x3=b(x2+x)3x3,函数过定点,则x2+x=0,即可求解;
(2)原抛物线顶点坐标为(![]() ,
,![]() ),平移后为(
),平移后为(![]() ,
,![]() ),即可求解;
),即可求解;
(3)根据题意分b>0和b<0,根据AB的长分别求出B点坐标,代入求出相应b的取值即可求解.
解:(1)y=bx2+(b3)x3=b(x2+x)3x3,
函数过定点,则x2+x=0,
解得x=0或x=1,
∴抛物线总会经过两个定点(0,3)、(1,0),
故答案为(0,3)、(1,0);
(2)原抛物线顶点横坐标为:![]() ,
,
纵坐标为:![]() ,
,
即(![]() ,
,![]() ),
),
平移后新抛物线顶点横坐标为:![]() ,纵坐标为:
,纵坐标为:![]() ,即(
,即(![]() ,
,![]() )
)
∴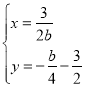
∴![]()
即为平移后的抛物线顶点所在的函数解析式为:![]() ;
;
(3)由![]() 与直线y=x–3交于点A(0,-3)
与直线y=x–3交于点A(0,-3)
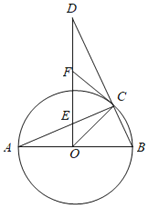
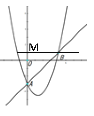
当b>0时,如图当AB=![]() 时,
时,
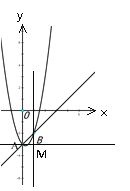
过点A作AM∥x轴,BM∥y轴交于点M
∵AM⊥BM,∠BAM=45°,AB=![]()
∴MA=MB=ABsin45°=1,
∴B(1,-2)
把B(1,-2)代入y=bx2+(b–3)x–3
得b=2.
AB=![]() 时,作BM⊥x轴交于点M
时,作BM⊥x轴交于点M
同理得AM=BM=4
∴B(4,1)
把B(4,1)代入y=bx2+(b–3)x–3 得b=![]() ,
,
![]() .
.
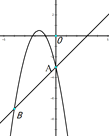
当![]() 时,
时,![]() ,同理可得
,同理可得![]() ,
,
代入![]() ,x无解;
,x无解;
当![]() ,同理可得B(-4,-7)
,同理可得B(-4,-7)
代入![]() 解得
解得![]()
∴![]() ,
,
综上,b的取值为![]() 或
或![]() .
.

【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
【题目】某数学拓展课研究小组经过市场调查,发现某种衣服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件160元,售价为x元,月销量为y件.
(1)求出y关于x的函数关系式;
(2)若销售该运动服的月利润为w元,求出w关于x的函数关系式,并求出月利润最大时的售价;
(3)由于运动服进价降低了a元,商家决定回馈顾客,打折销售,结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低10元,则a的值是多少?