题目内容
【题目】已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.
(1)△BEM与△AEC全等吗?请说明理由;
(2)BM与AC相等吗?请说明理由;
(3)求△ABC的面积.

【答案】(1)全等,理由见解析;(2)相等,理由见解析;(3)S△ABC=14.
【解析】
(1)根据已知条件易证AE=BE,再由AAS即可证明△BEM≌△AEC;(2)根据全等三角形的性质即可得BM=AC;(3)由(1)可知△BEM≌△AEC,根据全等三角形的性质可得BE=AE,EM=EC,再由三角形的面积公式计算即可.
(1)全等,
∵AE、BD为△ABC的高,
∴∠BEM=∠AEC=∠BDC=90°,
∴∠EBM+∠C=∠EBM+∠BME=90°,
∴∠BME=∠C,
又∠ABC=45°,
∴∠ABC=∠BAE=45°,
∴AE=BE,
在△BEM和△AEC中
∵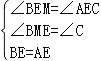
∴△BEM≌△AEC(AAS),
(2)相等,
∵△BEM≌△AEC,
∴BM=AC.
(3)∵△BEM≌△AEC,
∴BE=AE=4,EM=EC=3,
∴BC=BE+EC=7,
∴S△ABC=![]() ×7×4=14.
×7×4=14.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目







