题目内容
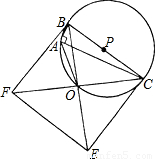
 如图:以O为圆心的同心圆中,大圆的弦AB切小圆于C,AB=10cm,则圆环的面积是
如图:以O为圆心的同心圆中,大圆的弦AB切小圆于C,AB=10cm,则圆环的面积是25πcm2
25πcm2
.分析:连接OA、OC,根据切线性质得出∠OCA=90°,根据垂径定理求出CA值,设两圆的半径分别为Rcm,rcm,由勾股定理求出R2-r2=9,求出两圆的面积的差即可得出答案.
解答:解:连接OA、OC,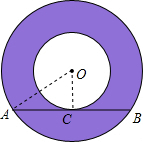
∵大圆的弦AB与小圆相切于点C,
∴∠OCA=90°,
由垂径定理得:AC=BC=
AB=5cm,
设两圆的半径分别为Rcm,rcm,(R>r)
则OA=R,OC=r,
∵由勾股定理得:R2-r2=AC2=52=25,
∴阴影部分的面积是πR2-πr2=π(R2-r2)=25π(cm2).
故答案为:25πcm2.

∵大圆的弦AB与小圆相切于点C,
∴∠OCA=90°,
由垂径定理得:AC=BC=
| 1 |
| 2 |
设两圆的半径分别为Rcm,rcm,(R>r)
则OA=R,OC=r,
∵由勾股定理得:R2-r2=AC2=52=25,
∴阴影部分的面积是πR2-πr2=π(R2-r2)=25π(cm2).
故答案为:25πcm2.
点评:本题考查了切线性质,垂径定理,勾股定理的应用.关键是求出R2-r2的值和根据图形得出阴影部分的面积=大圆的面积-小圆的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
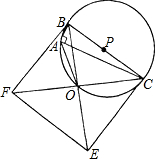 (1)求证:点O在⊙P上且∠BAO=135°;
(1)求证:点O在⊙P上且∠BAO=135°;
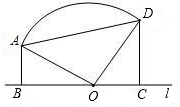
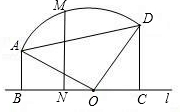


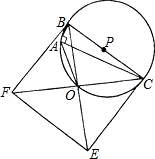 (1)求证:点O在⊙P上且∠BAO=135°;
(1)求证:点O在⊙P上且∠BAO=135°; ,求BO及AC的长.
,求BO及AC的长.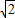 ,求BO及AC的长.
,求BO及AC的长.