题目内容
已知点O在直线l上, |
| AD |
(1)当点A、D在直线l的同侧时,试探索线段AB、BC、CD之间有怎样的等量关系?请写出你的结论并予以证明;当点A、D在直线l的两侧时,且AB≠CD时,线段AB、BC、CD之间又有怎样的等量关系?请直接写出结论(不必证明).
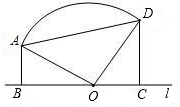
(2)如图,
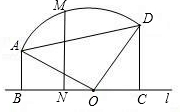
当点A、D在直线l的同侧,如果AB=3,CD=4,点M是
 |
| AD |
分析:(1)根据圆的性质可知OA=OD,根据已知可得∠ABC=∠OCD=∠AOD=90°,由余角的性质可得∠AOB=∠ODC
即可证得Rt△ABO≌Rt△OCD,可得AB+CD=BC;在两侧的证明方法一样,可求得BC=|AB-CD|.
(2)此题需要借助于辅助线,需要构造矩形与相似三角形,根据它们的性质求解即可,辅助线为过点A作AH⊥CD,垂足为点H,连接MO,可得矩形,又点M是弧
的中点,AD⊥OM,MN⊥BC,所以AH∥BC,即得MN⊥AH,∠DAH=∠OMN,即可证Rt△DAH∽Rt△OMN;根据相似三角形的性质即可求得.
即可证得Rt△ABO≌Rt△OCD,可得AB+CD=BC;在两侧的证明方法一样,可求得BC=|AB-CD|.
(2)此题需要借助于辅助线,需要构造矩形与相似三角形,根据它们的性质求解即可,辅助线为过点A作AH⊥CD,垂足为点H,连接MO,可得矩形,又点M是弧
 |
| AD |
解答:(1)解:AB+CD=BC.(1分)
①证:在Rt△ABO和Rt△OCD中,
∵∠BAO+∠AOC=90°,∠DOC+∠AOC=90°
∴∠BAO=∠DOC
∵OA=OD
∴Rt△ABO≌Rt△OCD(2分)
∴AB=OC,BO=CD
∴AB+CD=OC+BO=BC(2分)
即:AB+CD=BC
②BC=|AB-CD|.(2分)
(2)过点A作AH⊥CD,垂足为点H,连接MO(1分)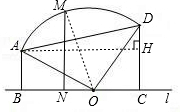
得:四边形ABCH为矩形,
∴AH=BC=AB+CD=7,DH=1
∴AD=
=
=5
∵AB=OC,
∴OD=
=
=5
∴OM=OD=5
∵点M是弧
的中点,
∴AD⊥OM
∵MN⊥BC,AH∥BC,
∴MN⊥AH
∴∠DAH=∠OMN
∴Rt△DAH∽Rt△OMN(2分)
∴
=
∴
=
∴MN=
(2分)
①证:在Rt△ABO和Rt△OCD中,
∵∠BAO+∠AOC=90°,∠DOC+∠AOC=90°
∴∠BAO=∠DOC
∵OA=OD
∴Rt△ABO≌Rt△OCD(2分)
∴AB=OC,BO=CD
∴AB+CD=OC+BO=BC(2分)
即:AB+CD=BC
②BC=|AB-CD|.(2分)
(2)过点A作AH⊥CD,垂足为点H,连接MO(1分)

得:四边形ABCH为矩形,
∴AH=BC=AB+CD=7,DH=1
∴AD=
| AH2+DH2 |
| 72+12 |
| 2 |
∵AB=OC,
∴OD=
| OC2+CD2 |
| 32+42 |
∴OM=OD=5
∵点M是弧
 |
| AD |
∴AD⊥OM
∵MN⊥BC,AH∥BC,
∴MN⊥AH
∴∠DAH=∠OMN
∴Rt△DAH∽Rt△OMN(2分)
∴
| AH |
| MN |
| AD |
| MO |
∴
| 7 |
| MN |
5
| ||
| 5 |
∴MN=
7
| ||
| 2 |
点评:此题考查了圆与相似三角形的性质与判定,解题的关键是要注意数形结合思想的应用,还要注意辅助线的作法,选择好辅助线会达到事半功倍的效果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•滨湖区一模)如图,AB是半圆O的直径,AB=10,过点A的直线交半圆于点C,且AC=6,连结BC,点D为BC的中点.已知点E在直线AC上,△CDE与△ACB相似,则线段AE的长为
(2013•滨湖区一模)如图,AB是半圆O的直径,AB=10,过点A的直线交半圆于点C,且AC=6,连结BC,点D为BC的中点.已知点E在直线AC上,△CDE与△ACB相似,则线段AE的长为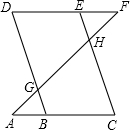 如图,已知点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF.∠C=∠D,则∠A与∠F相等吗?为什么?
如图,已知点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF.∠C=∠D,则∠A与∠F相等吗?为什么? 如图,已知点O在直线AB上,∠BOC=90°,则∠AOE的余角是( )
如图,已知点O在直线AB上,∠BOC=90°,则∠AOE的余角是( )