题目内容
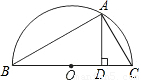
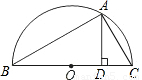
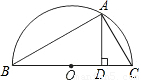
如图,以BC为直径作Rt△ABC的外接圆,圆心为点P,在△ABC的同侧又作正方形BCEF,BE、CF交于点为O,连接AO.(1)求证:点O在⊙P上且∠BAO=135°;
(2)如果AB=2,AO=4
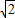 ,求BO及AC的长.
,求BO及AC的长.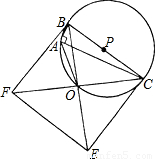
【答案】分析:(1)连接OP.根据正方形的性质、直角三角形的性质和圆周角定理的推论进行求解;
(2)过O作OK⊥BA延长线于K.根据等腰直角三角形的性质和勾股定理进行计算.
解答:(1)证明:连接OP.
∵四边形BCEF是正方形,
∴BE⊥CF,OB=OC.
∵P是BC的中点,
∴OP= BC.
BC.
∵BC是圆的直径,
∴点O在圆上.
∴∠BAO=90°+45°=135°.
(2)解:过O作OK⊥BA延长线于K.
∵AO=4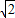 ,
,
∴∠BAO=135°,
∴∠OAK=45°,
∴AK=OK=4.
根据勾股定理,得
BO=2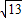 ,
,
∴AC=10.
点评:此题综合运用了正方形的性质、等腰直角三角形的性质和勾股定理.
(2)过O作OK⊥BA延长线于K.根据等腰直角三角形的性质和勾股定理进行计算.
解答:(1)证明:连接OP.
∵四边形BCEF是正方形,

∴BE⊥CF,OB=OC.
∵P是BC的中点,
∴OP=
 BC.
BC.∵BC是圆的直径,
∴点O在圆上.
∴∠BAO=90°+45°=135°.
(2)解:过O作OK⊥BA延长线于K.
∵AO=4
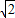 ,
,
∴∠BAO=135°,
∴∠OAK=45°,
∴AK=OK=4.
根据勾股定理,得
BO=2
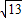 ,
,∴AC=10.
点评:此题综合运用了正方形的性质、等腰直角三角形的性质和勾股定理.

练习册系列答案
相关题目
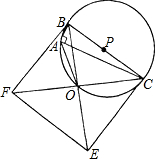 (1)求证:点O在⊙P上且∠BAO=135°;
(1)求证:点O在⊙P上且∠BAO=135°;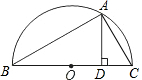 如图,以BC为直径作半圆,在半圆上取一点A,作AD⊥BC,D为垂足,若AB=2AC,那么BC:AD的值为
如图,以BC为直径作半圆,在半圆上取一点A,作AD⊥BC,D为垂足,若AB=2AC,那么BC:AD的值为