Question

【题目】如图，二次函数y=x2+bx+c的图象交x轴于A、D两点，并经过B点，已知A点坐标是（2，0），B点的坐标是（8，6）．

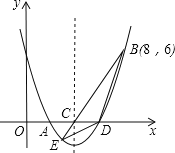
（1）求二次函数的解析式．

（2）求函数图象的顶点坐标及D点的坐标．

（3）该二次函数的对称轴交x轴于C点，连接BC，并延长BC交抛物线于E点，连接BD，DE，直接写出△BDE的面积．

Answer 1

【答案】（1）y=x2﹣4x+6；（2）顶点坐标为（4，﹣2），y=x2﹣4x+6；（3）．

【解析】

试题分析：（1）把A（2，0），B（8，6）代入y=x2+bx+c得到关于b、c的方程组，然后解方程组求出b、c即可得到抛物线解析式；

（2）先把（1）中的解析式配成顶点式即可得到顶点坐标，然后利用抛物线对称性确定D点坐标；

（3）先利用待定系数法求出直线BC的解析式，再利用解方程组得E点坐标，然后利用S△BDE=S△BDC+S△EDC进行计算即可．

解：（1）把A（2，0），B（8，6）代入y=x2+bx+c得，解得，

所以二次函数解析式为y=x2﹣4x+6；

（2）y=x2﹣4x+6=（x﹣4）2﹣2，

所以二次函数图象的顶点坐标为（4，﹣2），

由于抛物线的对称轴为直线x=4，而A（2，0），

所以D点坐标为（6，0）；

（3）C（4，0），

设直线BC的解析式为y=mx+n，

把B（8，6），C（4，0）代入得，解得，

所以直线BC的解析式为y=x﹣6，

解方程组得或，

所以E点坐标为（3，﹣），

所以S△BDE=S△BDC+S△EDC=×（6﹣4）×6+×（6﹣4）×=．