Question

【题目】如图1，等边△ABC中，点D、E、F分别为AB、BC、CA上的点，且AD=BE=CF．

（1）△DEF是__________三角形；

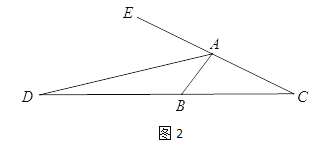
（2）如图2，M为线段BC上一点，连接FM，

在FM的右侧作等边△FMN，连接DM、EN．求证：DM=EN；

（3）如图3，将上题中“M为线段BC上一点”改为“点M为CB延长线上一点”，其余条件不变，求证：DM=EN．

Answer 1

【答案】（1）证明见解析（2）证明见解析（3）证明见解析

【解析】试题分析：（1）等边中， 可得除之外的三个三角形全等，所以的三条边相等．
（2）证明 证明即可．两个三角形分别有两边对应相等，只需求其夹角相等即可，即求
（3）即证明．同（2），只需求即可．

试题解析：证明：(1)∵是等边三角形，

∴为等边三角形.

故答案为：等边.

(2)由(1)得，DE=EF=DF，

(3)同理，DE=EF=DF，MF=MN=FN，

∴∠MFD=∠EFN，

∴△MDF≌△NEF，

∴DM=EN.