题目内容
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径。
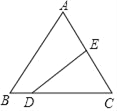
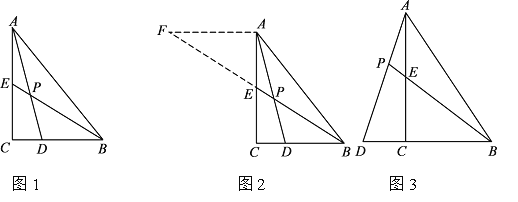
(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段AC,同时我们还发现损矩形中有公共边的两个三角形角的特点,在公共边的同侧的两个角是相等的。如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC。请再找一对这样的角来 =
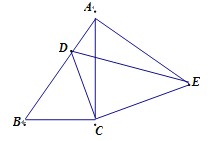
(2)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由。
(3)在第(2)题的条件下,若此时AB=![]() ,BD=
,BD=![]() ,求BC的长。
,求BC的长。

【答案】(1)∠ABD=∠ACD;(2)四边形ACEF为正方形,理由见解析;(3)5.
【解析】
(1)以AD为公共边,有∠ABD=∠ACD;
(2)证明△ADC是等腰直角三角形,得AD=CD,则AE=CF,根据对角线相等的菱形是正方形可得结论;
(3)如图2,作辅助线构建直角三角形,证明△ABC≌△CHE,得CH=AB=3,根据平行线等分线段定理可得BG=GH=4,从而得结论.
解:(1)由图1得:△ABD和△ADC有公共边AD,在AD同侧有∠ABD和∠ACD,此时∠ABD=∠ACD;
(2)四边形ACEF为正方形,理由是:
∵∠ABC=90°,BD平分∠ABC,
∴∠ABD=∠CBD=45°
∴∠DAC=∠CBD=45°
∵四边形ACEF是菱形,
∴AELCF,
∴∠ADC=90°,
∴△ADC是等腰直角三角形,
∴AD=CD,.AE=CF,
∴菱形ACEF是正方形;
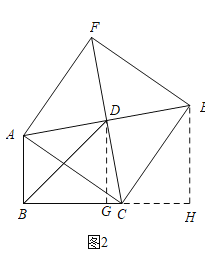
(3)如图2,过D作DG⊥BC于G,过E作EH⊥BC,交BC的延长线于H,
∵∠DBG=45°,
∴△BDG是等腰直角三角形,BD=4![]() ,
,
∵BG=4,四边形ACEF是正方形,
∴AC=CE,∠ACE=90°,AD=DE,
易得△ABC≌△CHE,
∴CH=AB=3,AB//DG//EH,AD=DE,
∴BG=GH=4,
∴CG=4-3=1,
∴BC=BG+CG=4+1=5.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案