Question

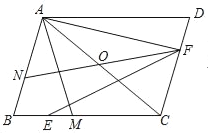
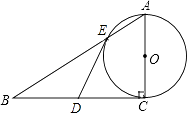
【题目】如图，在Rt△ABC中，∠ABC=90°，AB=6，D为AC中点，过点A作AE∥BC，连结BE，∠EBD=∠CBD，BD=5，则BE的长为________.

Answer 1

【答案】

【解析】

连接ED并延长交BC于点F，由AE//BC及点D是AC的中点，可证明△ADE≌△CDF，得AE=CF,DE=DF，结合∠EBD=∠CBD，可猜想BF=BE，则BE+AE=BC=8，在Rt△ABE中，由勾股定理构造关于BE的方程解答即可.

如图，连接ED并延长交BC于点F，过点D分别作DP⊥BE，垂足为P；作DQ⊥BC，垂足为Q,

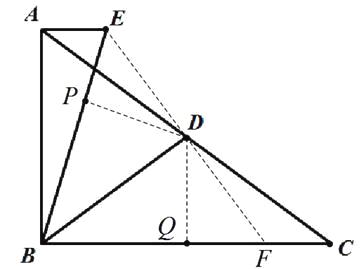
在Rt△ABC中，∵D是斜边AC的中点，

∴AD=CD=BD=5，AC=2BD=10，

∴，

∵AE//BC，

∴∠EAD=∠FCD，∠AED=∠CFD，

又∵AD=CD，

∴△ADE≌△CDF，

∴DE=DF，AE=CF，

又∵∠EBD=∠CBD， DP⊥BE， DQ⊥BC，

∴DP=DQ，

又∵BD=BD，DE=DF，

∴Rt△BDP≌Rt△BDQ（HL），Rt△PDE≌Rt△QDF（HL），

∴BP=BQ,PE=QF,

∴BF=BE，

∴BE+AE=BF+CF=BC=8,

设BE=x，则AE=8-x，

在Rt△ABE中，

由勾股定理得

得(8-x)2+62=x2，

解得x=,

即BE= .

故答案为：