题目内容
【题目】如图:直线AB、CD相交于点O;
(1)若∠AOC=30°,则∠BOC= °,∠BOD= °;
(2)将直线CD绕点O旋转,请根据下表所给数据将表格补充完整;
∠AOC | 60° | 90° | x° |
∠BOD |
|
|
|
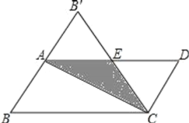
(3)如图3,过点O分别作∠AOC与∠AOD的角分线OE、OF,若∠BOD的度数为α,请用含α的代数式表示∠COF的度数.

【答案】(1)150°,30°.(2)60°,90°,x°.(3)∠COF=90°+![]() α.
α.
【解析】
(1)根据平角等于180°,利用角的和差即可得出答案;
(2)同(1)的计算方法即可得出答案;
(3)首先证明∠EOF=90°,利用(2)中结论求出∠EOC即可解决问题.
解:(1)如图1中,∵∠AOC=30°,
∴∠BOC=∠AOB-∠AOC
=180°-30°
=150°,
∠BOD=∠COD-∠BOC=180°﹣150°=30°,
故答案为150°,30°.
(2)由(1)可知∠AOC+∠BOC=180°,∠BOD+∠BOC=180°,
∴∠BOD=∠AOC(同角的补角相等),
∴当∠AOC=60°时,∠BOD=60°,
当∠AOC=90°时,∠BOD=90°,
当∠AOC=x°时,∠BOD=x°,
故答案为60°,90°,x°.
(3)∵∠AOC=∠BOD,∠BOD=α,
∴∠AOC=α,
∵OE平分∠AOC,
∴∠EOC=![]() α,
α,
∵OF平分∠AOD,
∴∠AOF=![]() ∠AOD,∠AOE=
∠AOD,∠AOE=![]() ∠AOC,
∠AOC,
∴∠EOF=∠AOE+∠AOF=![]() ∠COD=90°,
∠COD=90°,
∴∠COF=90°+![]() α.
α.

练习册系列答案
相关题目