题目内容
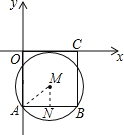
【题目】如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,﹣4),则圆心M的坐标为( )
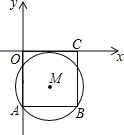
A.(﹣2,2.5) B.(2,﹣1.5) C.(2.5,﹣2) D.(2,﹣2.5)
【答案】D
【解析】
试题分析:过M作MN⊥AB于N,连接MA,设⊙M的半径是R,根据正方形性质求出OA=AB=BC=CO=8,根据垂径定理求出AN,得出M的横坐标,在△AMN中,由勾股定理得出关于R的方程,求出R,即可得出M的纵坐标.
解:∵四边形ABCO是正方形,A(0,﹣4),
∴AB=OA=CO=BC=4,
过M作MN⊥AB于N,连接MA,
由垂径定理得:AN=![]() AB=2,
AB=2,
设⊙M的半径是R,则MN=8﹣R,AM=R,由勾股定理得:AM2=MN2+AN2,
R2=(4﹣R)2+22,
解得:R=![]() ,
,
∵AN=2,四边形ABCO是正方形,⊙M于x轴相切,
∴M的横坐标是2,
即M(2,﹣![]() ).
).
故选D.

练习册系列答案
相关题目
【题目】甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路匀速驶向C城.已知A、C两城的距离为360km,B、C两城的距离为320km,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为xkm/h.
(1)根据题意填写下表:
行驶的路程(km) | 速度(km/h) | 所需时间(h) | |
甲车 | 360 |
|
|
乙车 | 320 | x |
|
(2)求甲、乙两车的速度.