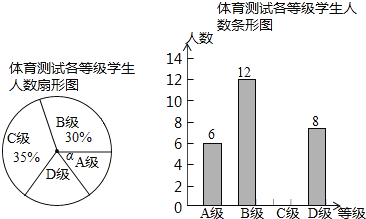
题目内容
【题目】如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.
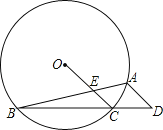
(1)求∠D的度数;
(2)若CE=3,AD=4,求线段AC的长.
【答案】(1)45°;(2)AC=2![]() .
.
【解析】
试题分析:(1)首先连接OC,由∠BAC=45°,易得△OBC是等腰直角三角形,又由AD∥OC,可求得∠D的度数;
(2)首先证得△ACE∽△DAC,然后由相似三角形的对应边成比例,求得答案.
解:(1)连接OB,
∵∠BOC=2∠BAC=90°,OB=OC,
∴∠OCB=∠OBC=45°,
∵AD∥OC,
∴∠D=∠OCB=45°;
(2)∵∠ABC=15°,∠OCB=45°,
∴∠AEC=60°,∠ACD=∠ABC+∠BAC=60°,
∴∠AEC=∠ACD=60°,
∵∠D=45°,∠ACD=60°,
∴∠CAD=75°,
又∵∠OCA=75°,
∴∠CAD=∠OCA=75°,
∴△ACE∽△DAC,
∴![]() =
=![]() ,
,
即AC2=ADCE=4×3=12,
∴AC=2![]() .
.


练习册系列答案
相关题目