题目内容
【题目】已知∠MON=90°,线段AB长为6cm,AB两端分别在OM、ON上滑动,以AB为边作正方形ABCD,对角线AC、BD相交于点P,连结OC.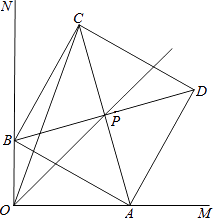
(1)求证:无论点A、点B怎样运动,点P都在∠AOB的平分线上;
(2)若OP=4 ![]() ,求OA的长.
,求OA的长.
(3)求OC的最大值(提示:取AB的中点Q,连接CQ、OQ,运用两点之间,线段最短)
【答案】
(1)
解:如图,作PE⊥OM、PF⊥ON垂足分别为E、F,
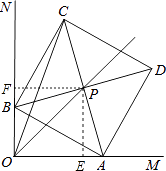
则∠PEA=∠PFB=90°=∠EOF,
∴∠EPF=90°,
∵ABCD是正方形,
∴PA=PB,且∠APB=90°,
∴∠APE+∠BPE=∠BPF+∠BPE,
即∠APE=∠BPF,
在△AEP和△BFP中,
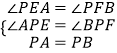 ,
,
∴△PAE≌△PBF(AAS),
∴PE=PF,
即点P在∠AOB的平分线上
(2)
解:∵四边形OEPF是正方形,OP=4 ![]() ,
,
∴OE=PE=4,
又∵Rt△APB中,AB=6,
∴PA=3 ![]() ,
,
∴Rt△AEP中,AE= ![]() =
= ![]() ,
,
∴OA=OE+AE=4+ ![]() 或OA=OE﹣AE=4﹣
或OA=OE﹣AE=4﹣ ![]()
(3)
解:如图,取AB的中点Q,连接OQ,CQ,OC,

∵AB长度不变,BC长度不变,
∴Rt△AOB中,OQ= ![]() AB=3,
AB=3,
Rt△BCQ中,CQ= ![]() =3
=3 ![]() ,
,
∵OQ+CQ≥OC,
∴当O,C,Q三点共线时,OC有最大值,
OC最大值=OQ+QC=3+3 ![]() .
.
【解析】(1)作PE⊥OM、PF⊥ON垂足分别为E、F,根据AAS判定△PAE≌△PBF,即可得出PE=PF,进而得到点P在∠AOB的平分线上;(2)根据四边形OEPF是正方形,OP=4 ![]() ,可得OE=PE=4,再根据Rt△APB中,AB=6,可得PA=3
,可得OE=PE=4,再根据Rt△APB中,AB=6,可得PA=3 ![]() ,进而得到Rt△AEP中,AE=
,进而得到Rt△AEP中,AE= ![]() ,据此可得OA的长;(3)取AB的中点Q,连接OQ,CQ,OC,根据AB长度不变,BC长度不变,可得Rt△AOB中,OQ=
,据此可得OA的长;(3)取AB的中点Q,连接OQ,CQ,OC,根据AB长度不变,BC长度不变,可得Rt△AOB中,OQ= ![]() AB=3,Rt△BCQ中,CQ=3
AB=3,Rt△BCQ中,CQ=3 ![]() ,再根据OQ+CQ≥OC,可得当O,C,Q三点共线时,OC有最大值,进而得到OC最大值=OQ+QC=3+3
,再根据OQ+CQ≥OC,可得当O,C,Q三点共线时,OC有最大值,进而得到OC最大值=OQ+QC=3+3 ![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案



