题目内容
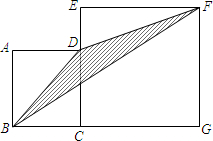 (2013•自贡模拟)如图,四边形ABCD和四边形EFBC均为正方形,点D在EC上.如果线段AB的长为5,则△BDF的面积为
(2013•自贡模拟)如图,四边形ABCD和四边形EFBC均为正方形,点D在EC上.如果线段AB的长为5,则△BDF的面积为12.5
12.5
.分析:设出正方形EFCG的边长为a,表示出ED与BG,求出三角形EFD的面积,由正方形EFCG的面积-三角形EFD的面积得到四边形DCGF的面积,求出三角形BCD的面积,三角形BDF面积=三角形BCD面积+四边形DCGF的面积-三角形BGF的面积,求出即可.
解答:解:设正方形EFGC的边长为a,即EC=EF=CG=FG=a,
∴ED=EC-DC=a-5,BG=BC+CG=a+5,
∴S△EFD=
a(a-5),
∴S四边形DCGF=a2-
a(a-5),
∵S△BCD=
×52=12.5,S△BCF=
a(a+5),
∴S△BDF=S△BCD+S四边形DCGF-S△BCF=12.5+a2-
a(a-5)-
a(a+5)=12.5.
故答案为:12.5.
∴ED=EC-DC=a-5,BG=BC+CG=a+5,
∴S△EFD=
| 1 |
| 2 |
∴S四边形DCGF=a2-
| 1 |
| 2 |
∵S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BDF=S△BCD+S四边形DCGF-S△BCF=12.5+a2-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:12.5.
点评:此题考查了整式的混合运算,弄清题意是解本题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
 (2013•自贡模拟)如图,⊙O中,点A、B、C都在⊙O上,如果∠B=30°,AC=
(2013•自贡模拟)如图,⊙O中,点A、B、C都在⊙O上,如果∠B=30°,AC=