题目内容
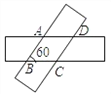
【题目】如图,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6cm,∠ABC=60°,则四边形ABCD的面积等于__________cm2.
【答案】![]()
【解析】
过点C作CE⊥AD,垂足为E. 过点C作CF⊥AB,垂足为F. (如图)
∵两张纸条的形状均为长方形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,即∠CBF=∠CDE,
∵两张纸条是等宽的,
又∵CF⊥AB,CE⊥AD,
∴CF=CE,
∵CF⊥AB,CE⊥AD,
∴∠CFB=∠CED=90°,
∵在△CFB与△CED中:
 ,
,
∴△CFB≌△CED (AAS),
∴CB=CD,
∴平行四边形ABCD为菱形,
∵AD=6cm,
∴AB=BC=CD=AD=6cm,
∵∠ABC=∠ADC,
又∵∠ABC=60°,
∴∠ADC=60°,即∠CDE=60°,
∴在Rt△CED中,∠DCE=30°,
∵CD=AD=6cm,
∴在Rt△CED中, ![]() cm,
cm,
∴在Rt△CED中, ![]() cm.
cm.
∵CE⊥AD,
∴四边形ABCD的面积为![]() cm2.
cm2.
故本题应填![]() .
.

练习册系列答案
相关题目