Question

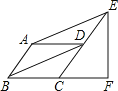
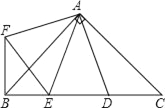
【题目】如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上的两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①∠EAF＝45°；②△AED≌△AEF；③△ABE∽△ACD；④BE2+DC2＝DE2．

其中正确的是______．（填序号）

Answer 1

【答案】①②④

【解析】

①根据旋转得到，对应角∠CAD＝∠BAF，由∠EAF＝∠BAF+∠BAE＝∠CAD+∠BAE即可判断

②由旋转得出AD=AF, ∠DAE＝∠EAF，及公共边即可证明

③在△ABE∽△ACD中，只有AB＝AC、∠ABE＝∠ACD＝45°两个条件，无法证明

④先由△ACD≌△ABF，得出∠ACD＝∠ABF＝45°，进而得出∠EBF=90°，然后在Rt△BEF中，运用勾股定理得出BE2+BF2=EF2，等量代换后判定④正确

由旋转，可知：∠CAD＝∠BAF．

∵∠BAC＝90°，∠DAE＝45°，

∴∠CAD+∠BAE＝45°，

∴∠BAF+∠BAE＝∠EAF＝45°，结论①正确；

②由旋转，可知：AD＝AF

在△AED和△AEF中，

∴△AED≌△AEF（SAS），结论②正确；

③在△ABE∽△ACD中，只有AB＝AC，、∠ABE＝∠ACD＝45°两个条件，

无法证出△ABE∽△ACD，结论③错误；

④由旋转，可知：CD＝BF，∠ACD＝∠ABF＝45°，

∴∠EBF＝∠ABE+∠ABF＝90°，

∴BF2+BE2＝EF2．

∵△AED≌△AEF，

EF＝DE，

又∵CD＝BF，

∴BE2+DC2＝DE2，结论④正确．

故答案为：①②④