题目内容
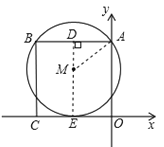
【题目】如图，在平面直角坐标系中，正方形ABCD的顶点A、C分别在y轴、x轴上，以AB为弦的⊙M与x轴相切．若点A的坐标为（0，8），则圆心M的坐标为 （ ）
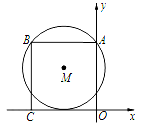
A．（-4，5） B．（-5，4） C．（-4，6） D．（-5，6）
【答案】A
【解析】
试题分析：过点M作
于D，连接AM，设
的半径为R，因为四边形OABC为正方形，定点A，C在坐标轴上，以边AB为弦的
与x轴相切，若点A的坐标为（0，8），所以
，
，AM=R，又因为
是直角三角形，利用勾股定理即可得到关于R的方程，解之即可．
过点M作于D，连接AM，设的半径为R，
∵以边AB为弦的与x轴相切，
，
∴
，
∴DE是直径的一部分；
∵四边形OABC为正方形，定点A，C在坐标轴上，点A的坐标为（0，8），
∴OA=AB=CB=OC=8，DM=8-R；
∴AD=BD=4（垂径定理）；
在
中
根据勾股定理可得
，
∴
∴R=5
∴M（-4，5）．
故选：A
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
