题目内容
完成推理填空:如图所示,已知AD=BC,AB=DC,试判断∠A与∠ABC的关系.下面是小颖同学的推导过程:
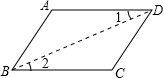 解:连接BD.在△ABD与△CDB中
解:连接BD.在△ABD与△CDB中
∵AD=CB (已知)
AB=CD (已知)
BD=DB (________)
∴△ABD≌△CDB (________)
∴∠1=∠2 (________)
∴AD∥BC (________)
∴∠A+∠ABC=180°(________)
公共边 SSS 两个三角形全等,对应角相等 内错角相等,两直线平行 两直线平行,同旁内角互补
分析:连接BD.在△ABD与△CDB中,根据全等三角形的判定定理SSS证明△ABD≌△CDB,然后由全等三角形的性质(对应角相等)知∠1=∠2;最后由平行线的判定定理(内错角相等,两直线平行)与性质(两直线平行,同旁内角互补)来求∠A与∠ABC的关系.
解答:连接BD.
在△ABD与△CDB中
∵AD=CB,AB=CD,BD=DB(公共边),
∴△ABD≌△CDB(SSS);
∴∠1=∠2(两个三角形全等,对应角相等),
∴AD∥BC (内错角相等,两直线平行),
∴∠A+∠ABC=180°(两直线平行,同旁内角互补).
故答案为:公共边;SSS;两个三角形全等,对应角相等;内错角相等,两直线平行;两直线平行,同旁内角互补.
点评:本题主要考查了全等三角形的判定与性质.解答此题时,通过构建全等三角形将已知和所求条件转化到相关的平行线中是解题的关键.
分析:连接BD.在△ABD与△CDB中,根据全等三角形的判定定理SSS证明△ABD≌△CDB,然后由全等三角形的性质(对应角相等)知∠1=∠2;最后由平行线的判定定理(内错角相等,两直线平行)与性质(两直线平行,同旁内角互补)来求∠A与∠ABC的关系.
解答:连接BD.
在△ABD与△CDB中
∵AD=CB,AB=CD,BD=DB(公共边),
∴△ABD≌△CDB(SSS);
∴∠1=∠2(两个三角形全等,对应角相等),
∴AD∥BC (内错角相等,两直线平行),
∴∠A+∠ABC=180°(两直线平行,同旁内角互补).
故答案为:公共边;SSS;两个三角形全等,对应角相等;内错角相等,两直线平行;两直线平行,同旁内角互补.
点评:本题主要考查了全等三角形的判定与性质.解答此题时,通过构建全等三角形将已知和所求条件转化到相关的平行线中是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
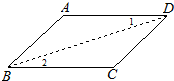 24、完成推理填空:如图所示,已知AD=BC,AB=DC,试判断∠A与∠ABC的关系.下面是小颖同学的推导过程:
24、完成推理填空:如图所示,已知AD=BC,AB=DC,试判断∠A与∠ABC的关系.下面是小颖同学的推导过程: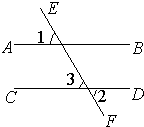 25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,
25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,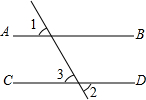 完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,
完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,