题目内容
【题目】如图,正方形OABC的顶点O是坐标原点,边OA和OC分别在x轴、y轴上,点B的坐标为(4,4).直线l经过点C.
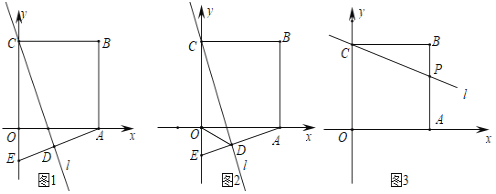
(1)若直线l与边OA交于点M,过点A作直线l的垂线,垂足为D,交y轴于点E.
①如图1,当OE=1时,求直线l对应的函数表达式;
②如图2,连接OD,求证:OD平分∠CDE.
(2)如图3,若直线l与边AB交于点P,且S△BCP=![]() S四边形AOCP,此时,在x轴上是否存在点Q,使△CPQ是以CP为直角边的直角三角形?若存在,求点Q的坐标,若不存在,请说明理由.
S四边形AOCP,此时,在x轴上是否存在点Q,使△CPQ是以CP为直角边的直角三角形?若存在,求点Q的坐标,若不存在,请说明理由.
【答案】(1)①y=﹣4x+4;②见解析;(2)存在,点Q(3,0)或(﹣2,0)
【解析】
(1)①由题意可求点A,点C坐标,用待定系数法可求直线AE解析式,由AE⊥直线l,可设直线l的解析式为y=﹣4x+m,将点C坐标代入,可求直线l的解析式;
②连接AC,由∠AOC=∠ADC=90°,可得点C,点A,点D,点O四点共圆,可得∠CAO=∠ODC=45°,即OD平分∠CDE;
(2)分∠PCQ=90°和∠CPQ=90°两种情况讨论,根据全等三角形的性质和相似三角形的性质可求点Q的坐标.
解:(1)①∵四边形OABC是正方形,点B(4,4)
∴点A(4,0),点C(0,4),
∴AO=CO=AB=BC=4,
∵OE=1
∴点E(0,﹣1)
设直线AE解析式为:y=kx+b,
∴![]()
解得:k=![]() ,b=﹣1,
,b=﹣1,
∴直线直线AE解析式为y=![]() x﹣1,
x﹣1,
∵AE⊥直线l,
∴设直线l的解析式为y=﹣4x+m,且过点C(0,4)
∴m=4,
∴直线l的解析式为y=﹣4x+4
②如图,连接AC,
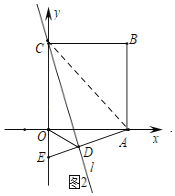
∵四边形OABC是正方形,
∴∠COA=90°,∠CAO=45°,
∵∠COA=∠CDA=90°,
∴点C,点A,点D,点O四点共圆,
∴∠CAO=∠ODC=45°
∴∠ODC=![]() ∠CDE
∠CDE
∴OD平分∠CDE
(2)存在
∵S△BCP=![]() S四边形AOCP,
S四边形AOCP,
∴S△BCP=![]() S正方形OABC,
S正方形OABC,
∴![]() ×4×BP=
×4×BP=![]() ×4×4,
×4×4,
∴BP=2,
∴AP=AB﹣BP=2,
如图,若∠PCQ=90°,
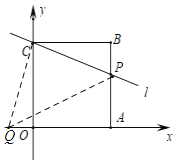
∴∠QCO+∠OCP=90°,
又∵∠BCO=∠BCP+∠OCP=90°,
∴∠QCO=∠BCP,且BC=CO,∠COQ=∠B=90°,
∴△BCP≌△OCQ(ASA)
∴BP=OQ=2
∴点Q(﹣2,0)
如图,若∠CPQ=90°,
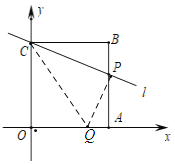
∴∠APQ+∠BPC=90°,
又∵∠BPC+∠BCP=90°,
∴∠BCP=∠APQ,且∠B=∠PAQ=90°,
∴△APQ∽△BCP
∴![]()
∴![]()
∴AQ=1,
∴OQ=AO﹣AQ=3,
∴点Q(3,0)
综上所述:点Q(3,0)或(﹣2,0)