题目内容
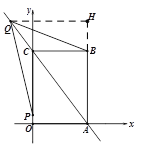
【题目】如图1,直线![]() ,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP, 连结PQ,设点P的坐标为P(0,t).
,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP, 连结PQ,设点P的坐标为P(0,t).
(1)求点B的坐标.
(2)若t=1时,连接BQ,求△ABQ的面积.
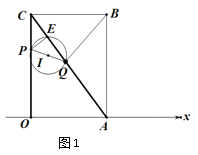
(3)如图2,以PQ为直径作⊙I,记⊙I与射线AC的另一个交点为E.
① 若![]() ,求此时t的值.
,求此时t的值.
② 若圆心I在△ABC内部(不包含边上),则此时t的取值范围为 .(直接写出答案)
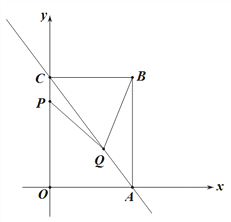
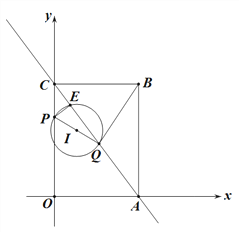
图1 图2
【答案】(1)B(6,8);(2)![]() ;(3)①
;(3)①![]() ,
, ![]() ,
, ![]() ,
, ![]() ;②
;②![]()
【解析】(1)解:将x=0代入![]() ,得y=8,∴C(0,8)
,得y=8,∴C(0,8)
将y=0代入![]() ,得x=6 ∴A(6,0)
,得x=6 ∴A(6,0)
∵矩形OABC ∴B(6,8)
(2) 作QH⊥AB于H,当t=1时,CP=7,AQ=14
易证AC=10, sin∠BAC=![]() ,
,
∴QH=AQsin∠BAC=![]()
∴S△ABQ=![]()
(3)分类:① 当P在线段OC上,Q在线段AC上时,即3<<8时,
如图1,易证![]() =sin∠EQP=sin∠ACO=
=sin∠EQP=sin∠ACO=![]() ,∴∠EQP=∠ACO∴CP=PQ
,∴∠EQP=∠ACO∴CP=PQ
∵PE⊥CQ,∴CE=EQ∴![]() 解得
解得![]()
②当Q与C重合,P在OC上时,如图2,可得16-2t=10,解得![]()
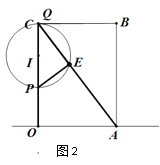
③当Q与C重合,P在OC延长线上时,如图3,可得2t-16=10,解得![]()
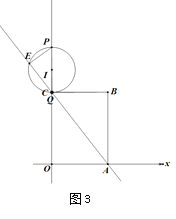
④当P在OC延长线上,Q在AC延长线上时,如图4,同①,可得∠Q=∠PCQ
∴CP=PQ∴![]() , 解得
, 解得![]()
∴![]()
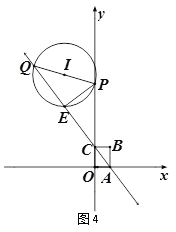
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目