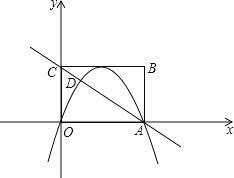
[题目]如图.在平面直角坐标系中.点A.B.C的坐标分别为．(1)请在图中画出△ABC向下平移3个单位的像△A′B′C′,(2)若一个二次函数的图象经过(1)中△A′B′C′的三个顶点.求此二次函数的关系式．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在平面直角坐标系中，点A，B，C的坐标分别为（0，2），（3，2），（2，3）．

（1）请在图中画出△ABC向下平移3个单位的像△A′B′C′；

（2）若一个二次函数的图象经过（1）中△A′B′C′的三个顶点，求此二次函数的关系式．

【答案】（1）作图见解析；（2）.

【解析】

（1）分别作出点A、B、C向下平移3个单位所得对应点，再顺次连接可得；

（2）根据题意写出A′，B′，C′的坐标，设过点A′，B′，C′的二次函数的关系式为y=ax2+bx+c，解方程组求出a、b、c的之即可．

（1）如图所示，△A′B′C′即为所求；

（2）由（1）知A′（0，-1）、B′（3，-1）、C′（2，0），

设抛物线解析式为y=ax2+bx+c，

则，

解得：，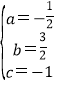

所以抛物线解析式为y=-x2+x-1．

练习册系列答案

(1)填空：a = ，b= ；

(2)求这所学校平均每班贫困学生人数；

(3)某爱心人士决定从2名贫困家庭学生的这些班级中，任选两名进行帮扶，请用列表或画树状图的方法，求出被选中的两名学生来自同一班级的概率．

贫困学生人数	班级数
1名	5
2名	2
3名	a
5名	1

【题目】点P为拋物线为常数，）上任意一点，将抛物线绕顶点G逆时针旋转90°后得到的图象与轴交于A、B两点（点A在点B的上方），点Q为点P旋转后的对应点．

（1）抛物线的对称轴是直线________，当m=2时，点P的横坐标为4时，点Q的坐标为_________；

（2）设点Q请你用含m，的代数式表示则________；

（3）如图，点Q在第一象限，点D在轴的正半轴上，点C为OD的中点，QO平分∠AQC，当AQ=2QC，QD=时，求的值．

【题目】如图，一架长2.5米的梯子AB斜靠在竖直的墙AC上，这时B到墙AC的距离为0.7米．

（1）若梯子的顶端A沿墙AC下滑0.9米至A1处，求点B向外移动的距离BB1的长；

（2）若梯子从顶端A处沿墙AC下滑的距离是点B向外移动的距离的一半，试求梯子沿墙AC下滑的距离是多少米？

【题目】如图，△ABC≌△ABD，点E在边AB上，CE∥BD，连接DE．

求证：（1）∠CEB=∠CBE；

（2）四边形BCED是菱形．

【题目】为响应“足球进校园”的号召，我县教体局在今年 11 月份组织了“县长杯”校园足球比赛．在某场比赛中，一个球被从地面向上踢出，它距地面的高度 h(m)可用公式 h＝﹣5t2+v0t 表示，其中 t(s)表示足球被踢出后经过的时间，v0(m/s)是足球被踢出时的速度，如果足球的最大高度到 20m，那么足球被踢出时的速度应达到________m/s．

【题目】已知：点P（m，4）在反比例函数y＝﹣的图象上，正比例函数的图象经过点P和点Q（6，n）．

（1）求正比例函数的解析式；

（2）求P、Q两点之间的距离．

【题目】（1）如图1，PA、PB是⊙O的两条弦，AB为直径，C为的中点，弦CD⊥PA于点E，写出AB与AC的数量关系，并证明；

（2）如图2，PA、PB是⊙O的两条弦，AB为弦，C为劣弧的中点，弦CD⊥PA于E，写出AE、PE与PB的数量关系，并证明．

【题目】如图，矩形OABC在平面直角坐标系xOy中，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=4，OC=3，若抛物线的顶点在BC边上，且抛物线经过O，A两点，直线AC交抛物线于点D．

（1）求抛物线的解析式；

（2）求点D的坐标；

（3）若点M在抛物线上，点N在x轴上，是否存在以A，D，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．

试题分类