��Ŀ����
����Ŀ����PΪ������![]() Ϊ������
Ϊ������![]() ��������һ�㣬���������ƶ���G��ʱ����ת90���õ���ͼ����
��������һ�㣬���������ƶ���G��ʱ����ת90���õ���ͼ����![]() �ύ��A��B���㣨��A�ڵ�B���Ϸ�������QΪ��P��ת��Ķ�Ӧ�㣮
�ύ��A��B���㣨��A�ڵ�B���Ϸ�������QΪ��P��ת��Ķ�Ӧ�㣮
��1��������![]() �ĶԳ�����ֱ��________����m=2ʱ����P�ĺ�����Ϊ4ʱ����Q������Ϊ_________��
�ĶԳ�����ֱ��________����m=2ʱ����P�ĺ�����Ϊ4ʱ����Q������Ϊ_________��
��2�����Q![]() �����ú�m��
�����ú�m��![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��![]() ________��
________��
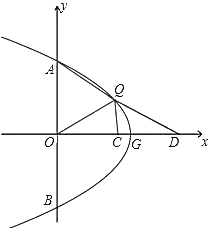
��3����ͼ����Q�ڵ�һ���ޣ���D��![]() ����������ϣ���CΪOD���е㣬QOƽ�֡�AQC����AQ=2QC��QD=
����������ϣ���CΪOD���е㣬QOƽ�֡�AQC����AQ=2QC��QD=![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
���𰸡���1��x=m��Q��-2,2������2��a=m-![]() ����3��m=1.
����3��m=1.
��������
��1���䷽���ɵó������ߵĶԳ���������m��ֵȷ����ԭ�����ߵĽ���ʽ�����������P��G����������P��PE��x����E����Q��QF��x����F��������ת������֪����GQF�ա�PGE����QF��GE��PE��GF���ɾݴ���õ�Q��������
��2����֪Q�����������ɵõ�QF��FG�ij������գ�1���ķ����������P��������Ȼ�����ԭ�����ߵĽ���ʽ���������a��b��m�Ĺ�ϵʽ��
��3���ӳ�QC��E��ʹ��QC��CE����ôAQ��QE����֤��QCD�ա�ECO����ôQD��OE��m����AQ��QE����QOƽ�֡�AQC����֤�á�AQO�ա�EQO����OA��OE��m����A������Ϊ��0��m����Ȼ��A��������루2���Ĺ�ϵʽ�����������m��ֵ��
��1��![]() =
=![]() ���Գ���Ϊֱ��x=m��
���Գ���Ϊֱ��x=m��
��m��2ʱ��y����x��2��2����G��2��0����
�ߵ�P�ĺ�����Ϊ4����P�������������ཫx��4���������߽���ʽ����y����4��2��2��4����P��4��4������ͼ������QG��PG������Q��QF��x����F������P��PE��x����E�����������ɵ�����GQF�ա�PGE����FQ��EG��2��FG��EP��4����FO��2����Q����2��2����

��2����֪Q��a��b������GE��QF��b��FG��m��a��
�ɣ�1��֪��PE��FG��m��a��GE��QF��b����P��m+b��m��a��������ԭ�����ߵĽ���ʽ��������m��a����m+b��2��2m��m+b��+m2��m��a��m2+b2+2mb��2m2��2mb+m2��a��m��b2�����ú�m��b�Ĵ���ʽ��ʾa��a��m��b2��
��3����ͼ���ӳ�QC����E��ʹCE��CQ������OE��
��CΪOD�е�����OC��CD��
�ߡ�ECO����QCD�����ECO�ա�QCD����OE��DQ��m��
��AQ��2QC����AQ��QE��
��QOƽ�֡�AQC�����1����2�����AQO�ա�EQO����AO��EO��m����A��0��m����
��A��0��m������ͼ��������0��m��m2����m1��1��m2��0���ᣩ����m��1��