题目内容
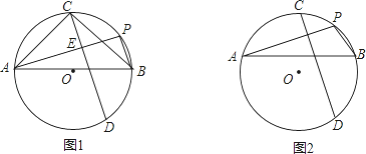
【题目】(1)如图1,PA、PB是⊙O的两条弦,AB为直径,C为![]() 的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
(2)如图2,PA、PB是⊙O的两条弦,AB为弦,C为劣弧![]() 的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
【答案】(1)AB=![]() AC(2)AE=PB+PE.
AC(2)AE=PB+PE.
【解析】
(1)AB=![]() AC.
AC.
证明:∵AB为直径,C为![]() 的中点,
的中点,
∴△ABC是等腰直角三角形.
∴AB=![]() AC.
AC.
(2)AE=PB+PE.
证明:在AE上截取AF=BP,连接AC、BC、FC、PC.
∵C为劣弧![]() 的中点,即
的中点,即![]() ,
,
∴AC=BC.
在△CAF和△CBP中,
∵AC=BC,∠CAF=∠CBP,AF=BP,
∴△CAF≌△CBP.
∴CF=CP.
∵CD⊥PA于E,
∴EF=EP.
∴AE=AF+EF=PB+PE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目