题目内容
【题目】如图所示,在∠AOB的两边上截取AO=BO,OC=OD,连接AD、BC交于点P,连接OP,则下列结论正确的是 ( )
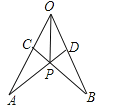
①△APC≌△BPD ②△ADO≌△BCO ③△AOP≌△BOP ④△OCP≌△ODP
A. ②③④ B. ①②③ C. ①②③④ D. ①③④
【答案】C
【解析】由AO=BO,OC=OD,∠O=∠O,可证得②△ADO≌△BCO,所以有∠COP=∠DOP,又OC=OD,OP=OP,可证得④△OCP≌△ODP,所以有PC=PD,又∠CAP=∠DBP,∠CPA=∠DBP可证得① △APC≌△BPO,所以有PA=PB,又AO=BO,OP=OP,可证得③ △AOP≌△BOP.
解:∵AO=BO,OC=OD,∠O=∠O,
∴△ADO≌△BCO(SAS),故②正确;
∴∠COP=∠DOP,
∵OC=OD,OP=OP,
∴△OCP≌△ODP(SAS),故④正确;
∴PC=PD,
∵∠CAP=∠DBP,∠CPA=∠DPB,
∴△APC≌△BPD(AAS),故①正确;
∴PA=PB,
∵AO=BO,OP=OP,
∴△AOP≌△BOP(SSS),故③正确.
故选C.

练习册系列答案
相关题目