题目内容
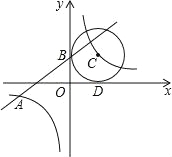
【题目】(2016浙江省舟山市第21题)如图,已知一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=![]() 的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
(1)、求m的值;
(2)、求一次函数的表达式;
(3)、根据图象,当y1<y2<0时,写出x的取值范围.
【答案】(1)、-1;(2)、y=![]() x+2;(3)、x<﹣4.
x+2;(3)、x<﹣4.
【解析】
试题分析:(1)、直接将A点代入反比例函数解析式求出答案;(2)、直接利用切线的性质结合正方形的判定与性质得出C,B点坐标,进而利用待定系数法求出一次函数解析式;(3)、利用A点坐标结合函数图象得出x的取值范围.
试题解析:(1)、把点A(﹣4,m)的坐标代入y2=![]() , 则m=4÷(-4)=﹣1, 得m=﹣1;
, 则m=4÷(-4)=﹣1, 得m=﹣1;
(2)、连接CB,CD, ∵⊙C与x轴,y轴相切于点D,B, ∴∠CBO=∠CDO=90°=∠BOD,BC=CD,
∴四边形BODC是正方形, ∴BO=OD=DC=CB, ∴设C(a,a)代入y2=![]() 得:a2=4,
得:a2=4,
∵a>0,∴a=2, ∴C(2,2),B(0,2),
把A(﹣4,﹣1)和(0,2)的坐标代入y1=kx+b中, 得:![]() , 解得:
, 解得:![]() ,
,
∴一次函数的表达式为:y1=![]() x+2;
x+2;
(3)/∵A(﹣4,﹣1),
∴当y1<y2<0时,x的取值范围是:x<﹣4.


练习册系列答案
相关题目