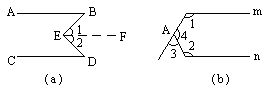题目内容
25、阅读下列解题过程:
如图,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数.
解:过E作EF∥AB,则AB∥CD∥EF(平行的传递性)
AB∥EF?∠B=∠1=35°
又因为CD∥EF?∠D=∠2=32°
所以∠BED=∠BED=∠1+∠235°+32°=67°(等量代换)
然后解答下列问题:
如图,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决:
问题(1):∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A=
问题(2):∠G+∠F+∠H=

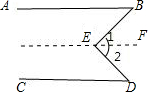
如图,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数.
解:过E作EF∥AB,则AB∥CD∥EF(平行的传递性)
AB∥EF?∠B=∠1=35°
又因为CD∥EF?∠D=∠2=32°
所以∠BED=∠BED=∠1+∠235°+32°=67°(等量代换)
然后解答下列问题:
如图,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决:
问题(1):∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A=
35°
;问题(2):∠G+∠F+∠H=
360
°时,GP∥HQ.

分析:本题主要利用两直线平行,同旁内角互补以及两直线平行内错角相等进行做题.
解答: 解:(1)由例题的结论可知,若AB∥DE,则∠A=∠ACD-∠D=65°-30°=35°;
解:(1)由例题的结论可知,若AB∥DE,则∠A=∠ACD-∠D=65°-30°=35°;
(2)过F作FE∥GP,若GP∥HQ,则FE∥GP∥HQ,
∠1+∠G=180°,∠2+∠H=180°,
∴∠1+∠2+∠G+∠H=360°,
即∠G+∠F+∠H=360°.
 解:(1)由例题的结论可知,若AB∥DE,则∠A=∠ACD-∠D=65°-30°=35°;
解:(1)由例题的结论可知,若AB∥DE,则∠A=∠ACD-∠D=65°-30°=35°;(2)过F作FE∥GP,若GP∥HQ,则FE∥GP∥HQ,
∠1+∠G=180°,∠2+∠H=180°,
∴∠1+∠2+∠G+∠H=360°,
即∠G+∠F+∠H=360°.
点评:两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
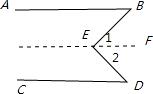
 (体验探究题)阅读下列解题过程并填空.
(体验探究题)阅读下列解题过程并填空.