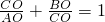题目内容
二次函数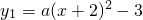 与
与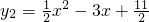 的图象的一个交点为A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C(点B在点C的左侧).则下列结论:
的图象的一个交点为A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C(点B在点C的左侧).则下列结论:
(1)无论x取何值,y2的值总是正数;(2)当x=0时,y2-y1=4;(3)当x≥-2时,y1、y2都随x的增大而增大;(4)2AB=3AC;
其中正确的是
- A.(1)(2)
- B.(2)(3)
- C.(1)(3)(4)
- D.(1)(4)
D
分析:把y2配成顶点式,根据二次函数的最值问题对①进行判断;把A点坐标代入y1,求出a确定y1的关系式,然后把x=0分别代入两个函数解析式中求出对应的函数值,再计算它们的差,则可对②进行判断;根据二次函数的增减性对③进行判断;根据抛物线的对称性确定B点和C点坐标,则可计算出AB与AC,然后对④进行判断.
解答:y2= (x-3)2+
(x-3)2+ ,则抛物线的顶点坐标为(3,
,则抛物线的顶点坐标为(3, ),而a=
),而a= >0,抛物线开口向上,则函数的最小值为
>0,抛物线开口向上,则函数的最小值为 ,所以①正确;
,所以①正确;
把A(1,3)代入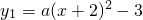 得9a-3=3,解得a=
得9a-3=3,解得a= ,则y1=
,则y1= (x+2)2-3,当x=0,y1=-
(x+2)2-3,当x=0,y1=- ,y2=
,y2= ,则y2-y1=
,则y2-y1= ,所以②错误;
,所以②错误;
当x≥-2时,y1随x的增大而增大;当x≥3时,y2随x的增大而增大,所以当x≥3时,y1、y2都随x的增大而增大,所以③错误;
因为y1= (x+2)2-3的对称轴为直线x=-2,所以B点坐标为(-5,3);因为y2=
(x+2)2-3的对称轴为直线x=-2,所以B点坐标为(-5,3);因为y2= (x-3)2+
(x-3)2+ 的对称轴为直线x=3,所以C点坐标为(5,3);则AB=6,AC=4,所以2AB=3AC,所以④正确.
的对称轴为直线x=3,所以C点坐标为(5,3);则AB=6,AC=4,所以2AB=3AC,所以④正确.
故选D.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-b2a;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.
分析:把y2配成顶点式,根据二次函数的最值问题对①进行判断;把A点坐标代入y1,求出a确定y1的关系式,然后把x=0分别代入两个函数解析式中求出对应的函数值,再计算它们的差,则可对②进行判断;根据二次函数的增减性对③进行判断;根据抛物线的对称性确定B点和C点坐标,则可计算出AB与AC,然后对④进行判断.
解答:y2=
 (x-3)2+
(x-3)2+ ,则抛物线的顶点坐标为(3,
,则抛物线的顶点坐标为(3, ),而a=
),而a= >0,抛物线开口向上,则函数的最小值为
>0,抛物线开口向上,则函数的最小值为 ,所以①正确;
,所以①正确;把A(1,3)代入
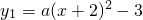 得9a-3=3,解得a=
得9a-3=3,解得a= ,则y1=
,则y1= (x+2)2-3,当x=0,y1=-
(x+2)2-3,当x=0,y1=- ,y2=
,y2= ,则y2-y1=
,则y2-y1= ,所以②错误;
,所以②错误;当x≥-2时,y1随x的增大而增大;当x≥3时,y2随x的增大而增大,所以当x≥3时,y1、y2都随x的增大而增大,所以③错误;
因为y1=
 (x+2)2-3的对称轴为直线x=-2,所以B点坐标为(-5,3);因为y2=
(x+2)2-3的对称轴为直线x=-2,所以B点坐标为(-5,3);因为y2= (x-3)2+
(x-3)2+ 的对称轴为直线x=3,所以C点坐标为(5,3);则AB=6,AC=4,所以2AB=3AC,所以④正确.
的对称轴为直线x=3,所以C点坐标为(5,3);则AB=6,AC=4,所以2AB=3AC,所以④正确.故选D.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-b2a;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.

练习册系列答案
相关题目
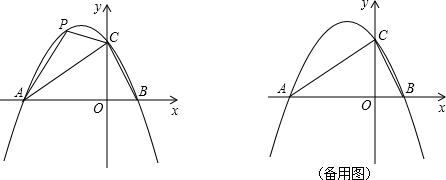
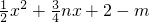 的图象与x轴交于A、B两点,与y轴交于点C,其中点A在点B的左边,若
的图象与x轴交于A、B两点,与y轴交于点C,其中点A在点B的左边,若