题目内容
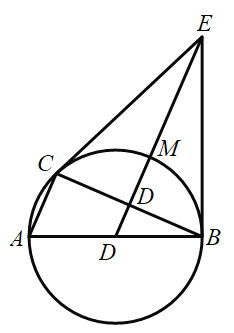
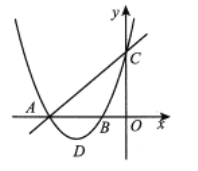
【题目】如图，直线
与
轴、
轴分别交于点
，
，经过，两点的抛物线
与轴的负半轴的另一交点为
，且
（1）求该抛物线的解析式及抛物线顶点
的坐标；
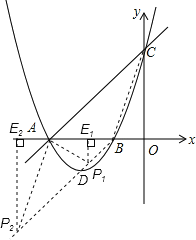
（2）点
是射线
上一点，问是否存在以点，，为顶点的三角形，与
相似，若存在，请求出点的坐标；若不存在，请说明理由
【答案】（1）
，顶点
；（2）存在，
或
【解析】
（1）利用直线解析式求出点A、C的坐标，从而得到OA、OC，再根据tan∠CBO=3求出OB，从而得到点B的坐标，然后利用待定系数法求出二次函数解析式，整理成顶点式形式，然后写出点D的坐标；
（2）根据点A、B的坐标求出AB，判断出△AOC是等腰直角三角形，根据等腰直角三角形的性质求出AC，∠BAC=45°，再根据点B、D的坐标求出∠ABD=45°，然后分①AB和BP是对应边时，△ABC和△BPA相似，利用相似三角形对应边成比例列式求出BP，过点P作PE⊥x轴于E，求出BE、PE，再求出OE的长度，然后写出点P的坐标即可；②AB和BA是对应边时，△ABC和△BAP相似，利用相似三角形对应边成比例列式求出BP，过点P作PE⊥x轴于E，求出BE、PE，再求出OE的长度，然后写出点P的坐标即可．
解：（1）令y=0，则x+3=0，
解得x=-3，
令x=0，则y=3，
∴点A（-3，0），C（0，3），
∴OA=OC=3，
∵tan∠CBO=
，
∴OB=1，
∴点B（-1，0），
把点A、B、C的坐标代入抛物线解析式得，
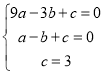，解得：
，
∴该抛物线的解析式为：，
∵y=x2+4x+3=（x+2）2-1，
∴顶点；
（2）∵A（-3，0），B（-1，0），
∴AB=-1-（-3）=2，
∵OA=OC，∠AOC=90°，
∴△AOC是等腰直角三角形，
∴AC=
OA=3，∠BAC=45°，
∵B（-1，0），D（-2，-1），
∴∠ABD=45°，
①AB和BP是对应边时，△ABC∽△BPA，
∴
，
即
，
解得BP=
，
过点P作PE⊥x轴于E，
则BE=PE=×
=
，
∴OE=1+=
，
∴点P的坐标为（-，-）；
②AB和BA是对应边时，△ABC∽△BAP，
∴
，
即
，
解得BP=
，
过点P作PE⊥x轴于E，
则BE=PE=×=3，
∴OE=1+3=4，
∴点P的坐标为（-4，-3）；
综合上述，当或时，以点
，
，
为顶点的三角形与
相似；
