题目内容
【题目】如图，已知直线y=﹣x和反比例函数 
（k＞0），点A（m，n）（m＞0）在反比例函数 上．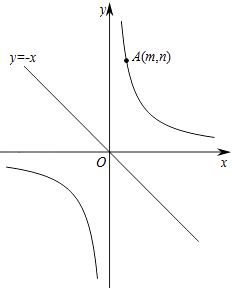
（1）当m=n=2时，
①直接写出k的值；
②将直线y=﹣x作怎样的平移能使平移后的直线与反比例函数 只有一个交点．
（2）将直线y=﹣x绕着原点O旋转，设旋转后的直线与反比例函数 交于点B（a，b）（a＞0，b＞0）和点C．设直线AB，AC分别与x轴交于D，E两点，试问： 
与 
的值存在怎样的数量关系？请说明理由．
【答案】
（1）
解：①当m=n=2时，A（2，2），
把点A（2，2）代入反比例函数 
（k＞0）得：k=2×2=4；
②设平移后的直线解析式为y=﹣x+b1，
由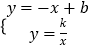 
可得， 
，
整理可得：x2﹣b1x+4=0，
当 
，即b1=±4时，方程x2﹣b1x+4=0有两个相等的实数根，此时直线y=﹣x+b1与反比例函数只有一个交点，
∴只要将直线y=﹣x向上或向下平移4个单位长度，所得到的直线与反比例函数只有一个交点
（2）
解： 
，理由如下：
分两种情况讨论：由反比例函数的对称性可知，C（﹣a，﹣b）
①当点A在直线BC的上方时，如图所示：
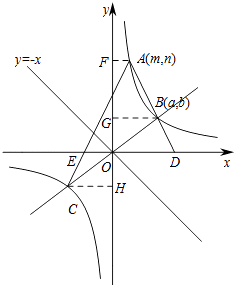
过A、B、C分别作y轴的垂线，垂足分别为F、G、H，
则OF=n，OG=OH=b，
∴FG=OF﹣OG=n﹣b，FH=OF+OH=n+b，
∵AF∥BG∥x轴，
∴ 
= 
= 
，
∵AF∥x轴∥CH，
∴ 
= 
= 
，
∴ + = + =2；
②当点A在直线BC的下方时，
同理可求： = 
， = ，
∴ ﹣ = ﹣ =2；
综上所述， ．
【解析】（1）①当m=n=2时，得出A（2，2），把点A（2，2）代入双曲线 （k＞0）求出k的值即可；
②设平移后的直线解析式为y=﹣x+b1 ， 由直线和双曲线解析式组成方程组，整理可得方程：x2﹣b1x+4=0，当判别式=0时，求出b1=±4即可；（2）分两种情况讨论：由双曲线的对称性可知，C（﹣a，﹣b），①当点A在直线BC的上方时，过A、B、C分别作y轴的垂线，垂足分别为F、G、H，则OF=n，OG=OH=b，得出FG=OF﹣OG=n﹣b，FH=OF+OH=n+b，由平行线得出比例式，即可得出结论；
②当点A在直线BC的下方时，同理可得出结论；即可得出结果．
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识，掌握反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点．
