题目内容
如图,P为正方形ABCD的边BC上的点,BP=3PC,Q是CD中点.
(1)求证:△ADQ∽△QCP;
(2)在现在的条件下,请再写出一个正确结论.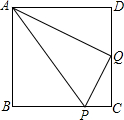
(1)求证:△ADQ∽△QCP;
(2)在现在的条件下,请再写出一个正确结论.

(1)证明:∵BP=3PC,
∴BC=BP+PC=4PC,
∵Q是CD中点,
∴CQ=DQ=
CD=
BC,
∴
=
=2,
又∵∠C=∠D=90°,
∴△ADQ∽△QCP;
(2)∵△ADQ∽△QCP,
∴∠DAQ=∠CQP,∠AQD=∠QPC,
也可得到∠AQP=90°.
所以,正确的结论可以是∠DAQ=∠CQP或∠AQD=∠QPC或∠AQP=90°(答案不唯一).
∴BC=BP+PC=4PC,
∵Q是CD中点,
∴CQ=DQ=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AD |
| CQ |
| DQ |
| CP |
又∵∠C=∠D=90°,
∴△ADQ∽△QCP;
(2)∵△ADQ∽△QCP,
∴∠DAQ=∠CQP,∠AQD=∠QPC,
也可得到∠AQP=90°.
所以,正确的结论可以是∠DAQ=∠CQP或∠AQD=∠QPC或∠AQP=90°(答案不唯一).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以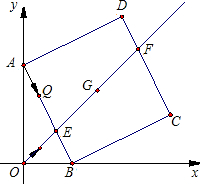 向以
向以
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.