Question

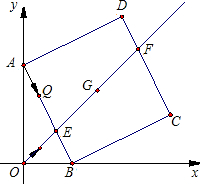
如图，G为正方形ABCD的对称中心，A（0，2），B（1，0），直线OG交AB于E，DC于F，点Q从A出发沿A→B→C的方向以

5

个单位每秒速度运动，同时，点P从O出发沿OF方向以

2

个单位每秒速度运动，Q点到达终点，点P停止运动，运动时间为t．求：
（1）求G点的坐标．
（2）当t为何值时，△AEO与△DFP相似？
（3）求△QCP面积S与t的函数关系式．

Answer 1

分析：（1）过C作CN⊥x轴于N，△ABO≌△BCN，推出C点的坐标，然后结合A、B两点的坐标即可推出G点的坐标；
（2）若想△AEO与△DFP相似，我们要先了解需要哪些条件，由于G是正方形的对称中心?∠GDF=45°，然后分两种情况进行讨论：∠DPF=45°时和当∠PDF=45°时，很容易即可推出t所的值；
（3）因为Q为运动的点，本题要根据Q点的不同位置分类求解：第一种情况为Q点在AE上时，第二种情况为Q点在EB上时，第三种情况为Q点在BC上时，根据三角形的面积公式，结合已知条件，分别求出△QCP面积S与t的函数关系式．

解答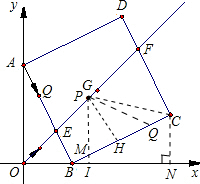：解：（1）过C作CN⊥x轴于N；由于四边形ABCD是正方形，
∴AB=BC，∠ABC=90°；
∴∠ABO+∠CBN=90°，
∵∠CBN+∠BCN=90°，
∴∠BCN=∠ABO，
∠AOB=∠BNC，
∴△ABO≌△BCN（aas），
则AO=BN=2，OB=CN=1，
∴C（3，1），
∵A（0，2），G为对角线AC的中点，
∴G（

3+0

2

，

1+2

2

）即G（

3

2

，

3

2

）；

（2）由于G是正方形的对称中心，
∴∠GDF=45°，
由于AB∥CD，得∠DFP=∠AEO，若△AEO与△DFP相似，则：
①当∠PDF=45°时，P、G重合，此时P（

3

2

，

3

2

），

2

t=

3

2

2

，
故t=

3

2

，
②∵A（0，2）B（1，0）C（3，1），
∴D（2，3），
当∠DPF=45°时，DP∥y轴，此时P（2，2），

2

t=2

2

故t=2；
所以当t=2或t=

3

2

时，△AEO与△DFP相似；

（3）0≤t≤

2

3

，
∵AQ=

5

t，
∴Q（t，2-2t），
∵OP=

2

t，
∴P（t，t），
∴PQ∥y轴，
∴PQ=2-2t-t=-3t+2，
∴高h=3-t，
∴S_△QCP=

1

2

（-3t+2）（3-t），
∴S=

3

2

t2-

11

2

t+3，
②

2

3

≤t≤1时，
PQ=3t-2，
∴S_△QCP=

1

2

（3t-2）（3-t），
∴S=-

3

2

t²+

11

2

t-3，
③1≤t≤2时，
如图，过P点作PH⊥BC，PI⊥x轴，垂足为H、I，PI交BC于M，
∴△BIM∽△PHM，
∵正方形ABCD，
∴∠ABO+∠MBI=90°，
∴∠OAB=∠MBI，
∴△BIM∽△ABO∽△PHM，
∵BI=t-1，
∴MI=

t-1

2

，PM=t-

t-1

2

=

t+1

2

，
∴PH=

2

5

PM=

2

5

×

t+1

2

=

t+1

5

，
∴S_△QCP=

1

2

(2

5

-

5

t)

t+1

5

=-

1

2

t2+

1

2

t+1，
∴S=

3 2 t2- 11 2 t+3(0≤t≤ 2 3 )    - 3 2 t2+ 11 2 t-3( 2 3 ≤t≤1) - 1 2 t2+ 1 2 t+1(1≤t≤2)

．

点评：本题主要考查相似三角形的判定与性质，三角形全等的性质，正方形的性质，二次函数式在实际问题中的综合应用，关键在于结合已知条件，求出各相关点的坐标，考虑Q点在不同位置时的分类求解．