题目内容
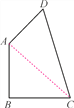
【题目】如图,在四边形ABCD中,AB=BC=1,CD=![]() ,DA=1,且∠B=90°.求:
,DA=1,且∠B=90°.求:
(1)∠BAD的度数;
(2)四边形ABCD的面积(结果保留根号).
【答案】(1)135°;(2)![]()
【解析】试题分析:(1)由于AB=BC=1,且∠B=90°根据勾股定理即可求出AC的长度,而CD=![]() ,DA=1,利用勾股定理的逆定理即可证明△ACD是直角三角形,由此即可求出∠BAD的度数;
,DA=1,利用勾股定理的逆定理即可证明△ACD是直角三角形,由此即可求出∠BAD的度数;
(2)首先把求四边形ABCD的面积分割为求△ABC和△ACD的面积,然后利用三角形的面积公式可以分别求出这两个三角形的面积,最后就可以求出四边形ABCD的面积.
试题解析:(1)∵AB=BC=1,且∠B=90°,
∴∠BAC=45°,AC=![]() ,
,
而CD=![]() ,DA=1,
,DA=1,
∴CD2=AD2+AC2,
∴△ACD是直角三角形,即∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=135°;
(2)∵S四边形ABCD=S△ABC+S△ACD,
而S△ABC=![]() AB×BC=
AB×BC=![]() ,
,
S△ACD=![]() AD×CD=
AD×CD=![]() ,
,
∴S四边形ABCD=S△ABC+S△ACD=![]()
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶汽车在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时) | 0 | 1 | 2 | 3 |
y(升) | 100 | 92 | 84 | 76 |
由表格中y与t的关系是____________.