Question

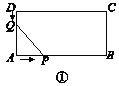
【题目】如图1，已知点A（﹣1，0），点B（0，﹣2），AD与y轴交于点E，且E为AD的中点，双曲线y=经过C，D两点且D（a，4）、C（2，b）．

（1）求a、b、k的值；

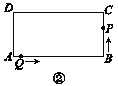
（2）如图2，线段CD能通过旋转一定角度后点C、D的对应点C′、D′还能落在y=的图象上吗？如果能，写出你是如何旋转的，如果不能，请说明理由；

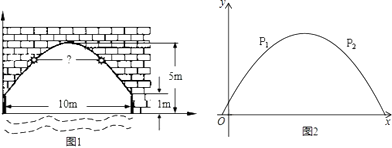
（3）如图3，点P在双曲线y=上，点Q在y轴上，若以A、B、P、Q为顶点的四边形为平行四边形，试求满足要求的所有点P、Q的坐标．

Answer 1

【答案】（1）；

（2）能. 当C、D绕点O顺时针旋转180°时，C’、D’落在图像上或点C、D关于原点中心对称的点在图像上；

（3）P1（1，4），Q1（0，6） P2（-1，-4），Q2（0，-6） P3（-1，-4），Q3（0，2）

【解析】试题（1）如图1，过点D做DP⊥y轴于点P，由△PDE≌△OAE（ASA），PD=OA，求出点D坐标，即可解决问题；（2）能，点C、D绕点O顺时针旋转180度时，点C′、D′落在图象上．或点C、D关于原点中心对称的点在图象上；（3）分两种情形分别求解①当AB为边时，如图1中，若四边形ABPQ为平行四边形，则；如图2中，若四边形ABQP是平行四边形时，AP=BQ，且AP∥BQ，求点P坐标，即可解决问题；②如图3中，当AB为对角线时，AP=BQ，AP∥BQ，求出点P坐标，即可解决问题．

试题解析：（1）如下图，过点D作DP⊥y轴交y轴于点P或过点D作x轴垂线

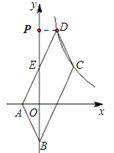
∵ E为AD的中点

∴ AE=DE

又∵ DP⊥y轴，∠AOE=90°，∠DPE=∠AEO，

∴△PDE≌△OAE(AAS)

∴ PD=OA

∵ A(-1，0)

∴ PD=1

∴ D点坐标为（1,4）

∵ 点D在反比例函数图像上

∴k=xy=1×4=4

∵点C在反比例函数图像上,C点坐标为（2，b)

∴即：

∴a=1,k=4,b=2

（2）能. 当C、D绕点O顺时针旋转180°时，C’、D’落在图像上

或点C、D关于原点中心对称的点在图像上

（3）∵由（1）知k=4，

∴反比例函数的解析式为，

∵点P在双曲线上，点Q在y轴上，

∴设Q（0，y），P（），

①当AB为边时：如下图所示：

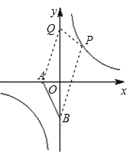
若ABPQ为平行四边形，则

解得x=1，此时P1（1，4），Q1（0，6）

如下图所示：

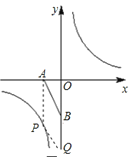
若ABQP为平行四边形，则，解得x=-1

此时P2（-1，-4），Q2（0，-6）

②如下图所示：

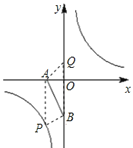
当AB为对角线时：AP=BQ，且AP∥BQ；

∴，解得x=-1

∴ P3（-1，-4），Q3（0，2）

故 P1（1，4），Q1（0，6） P2（-1，-4），Q2（0，-6） P3（-1，-4），Q3（0，2）