题目内容
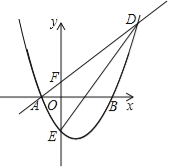
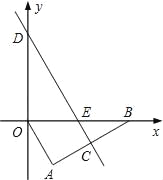
【题目】如图,在 Rt△OAB 中,∠A=90°,∠ABO=30°,OB=![]() ,边 AB的垂直平分线 CD 分别与 AB、x 轴、y 轴交于点 C、E、D.
,边 AB的垂直平分线 CD 分别与 AB、x 轴、y 轴交于点 C、E、D.
(1)求点 E的坐标;
(2)求直线 CD的解析式;
(3)在直线 CD上找一点Q使得三角形O,D,Q为等腰三角形,并求出所有的Q点;若不存在,请说明理由.
【答案】(1)E(![]() ,0);(2)y=﹣
,0);(2)y=﹣![]() x+2;(3)使得三角形 O,D,Q 为等腰三角形的Q 点 Z 坐标为 Q1(1,﹣
x+2;(3)使得三角形 O,D,Q 为等腰三角形的Q 点 Z 坐标为 Q1(1,﹣![]() +2),Q2(﹣1,
+2),Q2(﹣1,![]() +2),Q3(
+2),Q3(![]() ,1),Q4(
,1),Q4(![]() ,﹣1).
,﹣1).
【解析】
![]() 根据 DC 是 AB 垂直平分线,得出 C 点为 OB 的中点,再根据 OB 的值,即可求出点 E 的坐标;
根据 DC 是 AB 垂直平分线,得出 C 点为 OB 的中点,再根据 OB 的值,即可求出点 E 的坐标;
![]() 先过点C作 CH⊥x轴,在 Rt△ABO中,根据∠ABO 的度数和 OB 的值求出AB的长,再在 Rt△CBH 中,求出 OH 的值,得出点 D 的坐标,再设直线CD的解析式,得出 k,b的值,即可求出直线CD的解析式;
先过点C作 CH⊥x轴,在 Rt△ABO中,根据∠ABO 的度数和 OB 的值求出AB的长,再在 Rt△CBH 中,求出 OH 的值,得出点 D 的坐标,再设直线CD的解析式,得出 k,b的值,即可求出直线CD的解析式;
![]() 分三种情况讨论,分别根据Q点的不同位置求出Q的坐标即可.
分三种情况讨论,分别根据Q点的不同位置求出Q的坐标即可.
(1)∵DC 是 AB 垂直平分线,OA 垂直 AB,
∴C 点为 OB 的中点,
∵∠A=90°,∠DCB=90°,
∴OA∥CD,
∴E 为 OB 的中点,
∵![]()
∴![]()
∴![]()
(2)过点 C 作 CH⊥x 轴于点 H,
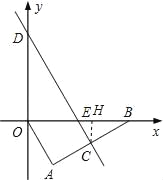
在 Rt△ABO 中,∠ABO=30°,![]()
![]()
![]()
又∵CD 垂直平分 AB,
∴BC=1,在 Rt△CBH 中,![]()
![]()
∴![]()
∴![]()
∵∠DGO=60°,
∴![]()
∴![]()
∴![]()
设直线 CD 的解析式为:y=kx+b,则,
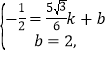
解得:![]() .
.
∴![]()
![]() 存在;
存在;
设![]() 有三种情况;
有三种情况;
当 OD=QD 时,
∵D(0,2),
![]() 即 4m2=22,解得;m=1 或 m=﹣1,
即 4m2=22,解得;m=1 或 m=﹣1,
∴![]()
当 OQ=DQ 时,则![]()
解得:![]()
![]()
当 OD=OQ 时,则 ![]() 解得:m=0,或
解得:m=0,或 ![]()
∴![]()
∴使得三角形 O,D,Q 为等腰三角形的Q 点 Z 坐标为![]()
![]()

 阅读快车系列答案
阅读快车系列答案